La integral definida
En el capítulo anterior hemos visto, cómo podemos aproximarnos al área de una región limitada por la gráfica de una función positiva, el eje de abscisas y dos rectas verticales, calculando las áreas de una serie de rectángulos que acotan el valor que buscamos. Disponemos de dos tipos de acotaciones: una superior (o por exceso) a la que hemos llamado suma superior (Sn) y otra inferior (o por defecto) a la que hemos llamado suma inferior (sn), de manera que si llamamos A al valor del área buscada se cumple
sn< A < Sm
siendo n y m dos números naturales cualesquiera. En el ejemplo anterior, además, para un mismo valor n, la diferencia entre suma superior y suma inferior Sn-sntiende a cero cuando n tiende a infinito. Esto último no es cierto en general con cualquier función, aunque sí lo es siempre que la función de partida sea continua en el intervalo en el que se está calculando el área.
Generalicemos un poco la situación anterior. Consideremos una función continua en un intervalo cerrado [a,b], no importando que no sea siempre positiva. Contesta a las siguientes cuestiones referentes a la gráfica adjunta.
El resultado del ejercicio anterior
nos muestra que el proceso seguido no siempre produce como resultado el
área de una figura plana. Sin embargo, también muestra que
si la diferencia entre las sumas superiores y las inferiores tiende a cero
ambas se acercan a un determinado número cuando n tiende a infinito.
En ese caso se dice que la función es integrable
en el intervalo [a,b] y el número obtenido recibe el nombre de integral
de la función f(x) en el intervalo [a,b].
Simbólicamente ese número
se escribe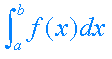 
. Cuando la función f(x) es positiva en el intervalo [a,b] (como
sucedía en el capítulo anterior) la integral coincide con
el área de la región limitada por la gráfica de la
función, el eje de abscisas, y las rectas x=a, x=b. Si f(x) no es
positiva eso no es cierto.
 |
 |
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||