

Triángulos oblicuángulos. Casos de resolución (continuación)
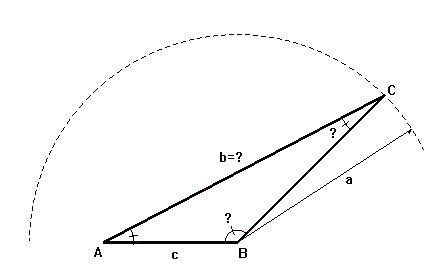
Supongamos conocidos los lados a y c y el ángulo A; quedarían como incógnitas el lado b y los ángulos B y C.
En primer lugar se aplica el teorema del seno.
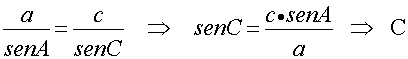
Ya estamos en condiciones de conocer el ángulo que falta, B.
![]()
Por último volvemos a aplicar el teorema del seno y calculamos el lado b.
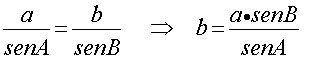
Pues bien, se nos pueden dar, en este último caso, las siguientes posibilidades:
a < c.sen A, con lo cual el triángulo no existe.
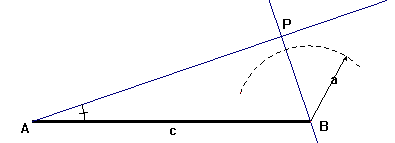
a = c.sen A, con lo cual el triángulo es rectángulo.
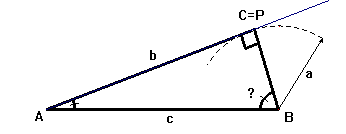
a > c.sen A y a< c, en cuyo caso existen dos triángulos: ABC y ABC´.
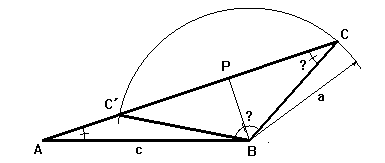
a>c.sen A y a>=C, con lo cual estamos en el caso de un sólo triángulo. Será esta posibilidad la que ocupe nuestro estudio dentro del caso IV.
|
|||||||||||||||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.