

ALGUNOS TEOREMAS BÁSICOS DE GEOMETRÍA
Teorema de Ceva
Teorema de Menelao
Teorema de Desargues
Teorema de Pappus
Teorema del hexagrama "místico" de Pascal
_______________________________________________________________________________________________________________
Entre los resultados más simples de la Geometría, están los llamados teoremas de configuración en los que se trata de un número finito de puntos y de rectas, así como de su pertenencia recíproca.
En general pueden formularse del siguiente modo:
Si algunos puntos pertenecen a una recta (o algunas rectas pasan por un punto) entonces algunos otos puntos están en una recta (o algunas otras rectas pasan por un punto).
Algunos de estos resultados se estudian en los cursos de Geometría elemental, al tratar los puntos y rectas notables de un triángulo. Algunos constituyen el fundamento para la Geometría Proyectiva. Son especialmente útiles para la resolución de problemas referentes a la construcción con diferentes restricciones como por ejemplo el trazado de figuras en una parte limitada del plano, con puntos inaccesibles.
Teoremas de Menelao y Ceva:
Los teoremas de Menelao y Ceva, en sus versiones originales son antiguos; uno data de la Grecia antigua y el otro de 1.678
Menelao de Alejandría fue un astrónomo griego que vivió en el primer siglo d. de C. Aunque sus obras en el griego original no han llegado a nosotros, sabemos de algunas de ellas por las observaciones que han hecho estudiosos posteriores y su tratado de tres libros Sphoerica , que se ha conservado hasta nuestros días en árabe. Este trabajo arroja considerable luz sobre el desarrollo griego de la trigonometría.
El teorema de Ceva está estrechamente relacionado con el de Menelao. Ambos son potentes herramientas que permiten tratar elegantemente muchos problemas en los que interviene la colinealidad de puntos y la concurrencia de rectas.
Aunque el teorema de Ceva está estrechamente relacionado con el de Menelao, parece que su descubrimiento fue eludido hasta 1.678, cuando el italiano Giovanni Ceva (1.647-1.736) publicó un trabajo que contenía tanto este teorema como el teorema de Menelao.
Definiciones:
Un punto que esté en un lado de un triángulo, pero que no coincida con ningún vértice, se llamará punto de Menelao del triángulo para dicho lado.
Una recta que pase por un vértice de un triángulo pero que no coincida con ningún lado, se llamará recta ceviana del triángulo para dicho vértice.
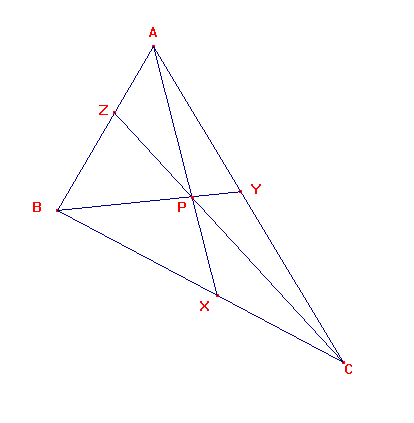
Teorema de Ceva:
Sea ABC un triángulo cualquiera y sean AX, BY y CZ tres cevianas.
Las tres cevianas son concurrentes si y sólo si se verifica:
![]()
1.- Experimenta trazando distintas cevianas.
2.- Comprueba la veracidad del teorema.
3.- Demuestra mediante este teorema que las 3 medianas de un triángulo se cortan en un punto.
Teorema de Menelao:
Los puntos X, Y, Z situados en los lados BC, CA y AB de un triángulo (o en sus prolongaciones) están alineados si y solamente si:
![]()
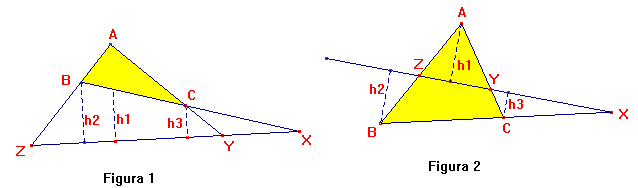
1.- Experimenta en el caso de que los tres puntos X,Y,Z se encuentren en las prolongaciones de los lados.
2.- Experimenta en el caso de que sólo uno de los puntos X,Y,Z esté fuera del triángulo.
3.- Comprueba la veracidad del teorema.
Para profundizar:
4.- Demuestra que las bisectrices exteriores de los tres ángulos de un triángulo escaleno cortan a sus tres respectivos lados opuestos en tres puntos que están alineados.
5.- Demuestra que las bisectrices interiores de dos ángulos de un triángulo escaleno y la bisectriz exterior del tercer ángulo cortan a sus respectivos lados opuestos en tres puntos que están alineados.
|
Para ir a la siguiente página pulsar aquí. |
|
|||||||||||||||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.