INECUACIONES LINEALES CON DOS INCÓGNITAS

Una inecuación lineal con dos incógnitas es cualquier desigualdad que, directamente o mediante transformaciones de equivalencia, se pueden expresar de una de las formas siguientes:

ax+by+c>0;     ax+by+c< 0;     ax+by+c0       ó        ax+by+c0

con a, b y c reales y a0, b0

La solución general está formada por el conjunto de todos los pares (s₁,s₂) que verifican la inecuación.

Gráficamente, la solución, son los puntos del plano que tienen por coordenadas (s₁,s₂).

Para resolver esta inecuación recurrimos a la ecuación ax+by+c=0, que es la ecuación de una recta y que, para cada uno de sus puntos, tiene por ordenada.

La inecuación anterior, mediante transformaciones de equivalencia, se puede expresar, dependiendo del signo de relación, como , es decir, la verifican todos los puntos que tiene una ordenada inferior(superior ó igual, según el sigo de relación) que la ordenada de los puntos de la recta. Por lo tanto, la solución general de una inecuación lineal con dos incógnitas es un semiplano, del que la recta anterior es su frontera.

 

Ejemplo:

resuelve x-3y-3 0

1. situamos en el plano la recta de ecuación   

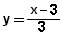
2. el semiplano solución viene dado por los puntos cuya ordenada es , es decir, los puntos del semiplano superior, incluyendo la recta

Escena 1

Puedes desplazar el puntos P arrastrándolo con el ratón.

0, para escribir <
1, para escribir (en la escena se escribe < =)
2, para escribir >
3, para escribir (en la escena se escribe > =)

¿Cuántas soluciones tiene la inecuación ?

Como puedes comprobar, al desplazar el punto P, las soluciones forman un semiplano, que será cerrado o abierto dependiendo de si es una desigualdad estricta o no.

Escena 2

repite la inecuación de la escena anterior, en esta, para ver el semiplano solución

Ficha 9