

RECTAS ÁNGULOS y CIRCUNFERENCIAS
2.- Ángulos centrales e inscritos
Ángulo central: Es la medida angular de un arco PQ de circunferencia, tomando como vértice el centro de la circunferencia.
Ángulo inscrito: Aquel cuyo vértice está sobre la circunferencia y cuyos lados pasan por dos puntos P y Q de ella.
La medida de un ángulo A inscrito en una circunferencia es la mitad del arco PQ que abarca, es decir la mitad del ángulo central correspondiente
1.- Utiliza el ratón para variar la abertura del arco PQ abarcado por el ángulo inscrito A. Observa que la medida de A es la mitad del arco PQ.
Visualiza el ángulo central correspondiente (cambia a 1 el valor de la casilla inferior). Su medida es la medida del arco PQ
2.- Dibuja en tu cuaderno, en una misma circunferencia, distintos ángulos inscritos de 45º
3.- Aprovecha lo que has aprendido para calcular en la siguiente figura, los ángulos CAD, ADB, ADV y AVD sabiendo que los arcos AB y CD miden respectivamente 100º y 40º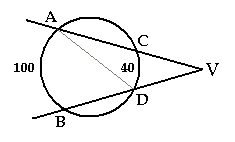
Un interesante caso particular
Cuando los puntos P y Q que forman el arco PQ son diametralmente opuestos, el arco que forman abarca 180º(media circunferencia) y por tanto el ángulo inscrito A con extremos en P y Q mide 90º, formando así un ángulo recto.
4.- Puedes mover con el ratón la posición del ángulo inscrito A o modificar el diámetro cambiando el valor de la casilla inferior. En todo momento la amplitud de A permanece constante e igual a 90º. Pulsa el botón animar para verlo más fácilmente.
5.- Dibuja en tu cuaderno un triángulo ABC inscrito en una circunferencia. Si A y B ocupan los extremos de un diámetro y el arco AC abarca la sexta parte de la circunferencia, ¿qué podemos decir del triángulo ABC?, ¿cuánto miden sus ángulos?
|
|||||||||||||||