Para calcular la proyección de un punto P(p.x, p.y) sobre una r ≡ Ax+By+C=0, basta con trazar la perpendicular a r por el punto P. La proyección Q se obtiene como intersección de ambas rectas. Para calcular sus coordenadas resolvemos el sistema de ecuaciones determinado por las ecuaciones de ambas rectas. A este punto Q también se conoce como el pie de la perpendicular trazada a r por el punto P.
Veámoslo con un ejemplo sobre el gráfico:
Ejemplo 1.- Calcula la proyección del punto P(4,5) sobre la recta r ≡ 2x+3y-8=0. Pasos a seguir: 1.- Calcula la perpendicular a r por el punto P. 2.- Halla el punto Q intersección de ambas rectas. Para ello resolvemos el sistema planteado por ambas ecuaciones.
Si atendemos a la escena podemos observar que podemos cambiar la ecuación de la recta r ≡ Ax+By+C=0. y el punto P(p.x,p.y) modificando los valores de A, B, C, p.x y p.y , o bien moviendo el punto P directamente.
|
|
Ejercicio 1.-
a) Calcula la proyección del punto P(1,2) sobre la recta r ≡ 2x-5y-14=0.
b) Calcula las proyecciones del punto P(4,5) sobre los ejes coordenados (Eje OX≡ y=0 --> A=0, B=1 y C=0. Eje OY ≡ x=0 --> A=1, B=0 y C=0). ¿Cómo varían las coordenadas del punto respecto de cada una de sus proyecciones sobre los ejes coordenados?.
c) Calcula la proyección del origen de coordenadas respecto de la recta y=5. (A=0, B=1 y C=-5)
Para calcular el simétrico P ' de un punto P(p.x, p.y) respecto de una recta r ≡ Ax+By+C=0, basta con tener en cuenta que el punto Q proyección de P sobre r, es el punto medio del segmento P P' . Según esto, lo primero que tendremos que hacer es calcular el punto Q como la proyección de P sobre r, y posteriormente calcular P ' utilizando la siguiente expresión: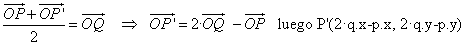
Veámoslo con un ejemplo sobre el gráfico.
Ejemplo 2.- Calcula el simétrico del punto P(4,5) respecto de la recta r ≡ 2x+3y-8=0. Pasos a seguir: 1.- Calcula la perpendicular a r por el punto P. 2.- Halla el punto Q intersección de ambas rectas. 3.- Cálculo de P ' . utilizando la expresión anterior P '(2·q.x-p.x,2·q.y-p.y)=(2·1'69-4,2·1,53-5)=(-0'61,-1,93). Si atendemos al gráfico podemos observar que podemos cambiar la ecuación de la recta r ≡ Ax+By+C=0. y del punto P(p.x,p.y) dándoles valores a A, B, C y a p.x y p.y respectivamente. O bien moviendo el punto P directamente.
|
|
Ejercicio 2.-
a) Calcula el simétrico del punto P(1,2) respecto de la recta r ≡ 2x-5y-14=0.
b) Calcula el simétrico del punto P(8,5) respecto de los ejes coordenados (x=0 e y=0). ¿Cómo varian las coordenadas del punto respecto de cada una de sus simétricos anteriores?.
c) Calcula el simétrico del origen de coordenadas respecto de la recta y-5=0.
d) ¿Sabrías calcular mentalmente cuales son las coordenadas del simétrico del origen de coordenadas respecto de la recta x=5?.
e) ¿Cuál sería el simétrico de un punto que estuviese contenido en la recta?. Compruébalo calculando el simétrico del punto P(1,1) respecto de la bisectriz del primer y tercer cuadrante (x-y=0).
Para calcular la ecuación de la recta simétrica de una recta s≡ A'x+B'y+C'=0 respecto de otra recta r ≡ Ax+By+C=0, que nos sirve de eje de simetría, bastará con tomar 2 puntos cualesquiera de la recta s y, aprovechando la construcción del apartado anterior, calcular el simétrico de estos dos puntos y posteriormente, la ecuación de la recta que pasa por ellos.
Veámoslo con en el siguiente ejemplo sobre el gráfico.
Ejemplo 3.- Determina la ecuacion de la recta simétrica de s≡-7x+8y-49=0 respecto de la rectarecta r ≡ 2x+3y-8=0. Pasos a seguir: 1.- Tomamos 2 puntos cualesquiera de la recta s, por ejemplo, los puntos de corte de s con los ejes coordenados, que serían P(0,6.13) y R(-7,0). 2.-Utilizando el apartado anterior ,halla los simétricos de P y R que son P'(-3.19,1.33) y R'(-3,61,5,07). 3.- Halla la ecuación de la recta que pasa por P' y R'. Si atendemos al gráfico podemos observar que podemos modificar las ecuaciónes de ambas rectas r≡ Ax+By+C=0. y s s≡ A'x+B'y+C'=0. Dándoles valores a A, B, C y a A', B' y C' respectivamente. |
|
Ejercicio 3.-
a) Determina la ecuación de la recta simétrica de s≡ x+y-1=0 respecto de la recta r≡ x-2y+3=0.
b) ¿Qué pasaría si las rectas r y s fueran paralelas?. ¿ Sabrías calcular mentalmente la ecuación de la recta simétrica de s≡ y=3 respecto del eje OX (y=0)?. ¿O la recta simétrica de x=5 respecto del eje OY (x=0)?.
c) ¿Recuerdas la condición de paralelismo A/A´= B/B´≠C/C´? Determina la ecuación de la recta simétrica de s≡ x-2y-1=0 respecto de la recta r≡ x-2y+3=0.
d) ¿Qué pasaría si las rectas r y s fuesen perpendiculares?. Calcula la recta simétrica del eje OX respecto del eje OY y viceversa.
e) ¿Recuerdas la condición de perpendicularidad A·A´+ B·B´=0?. Calcula la ecuación de la recta simétrica de s≡ -3x+2y-8=0 respecto de r≡ 2x+3y+8=0.
Para calcular la proyección de un punto P(p.x, p.y) respecto de la recta r según la dirección de un vector V(v1, v2) tendremos que calcular la ecuación de una recta s que pasa por P y tenga la dirección del vector V. La intersección de ambas rectas nos dará la proyección Q. Una vez obtenido Q, podemos obtener P' simétrico de P según V, considerando que Q es el punto medio del segmento PP'. Una vez obtenido P' calculamos P" como simétrico(simetría ortogonal) de P' respecto de la recta r.
Veámoslo en el siguiente ejemplo:
Ejemplo 4.- Calcula la proyección, simétrico y reflejado del punto P(4,5) respecto de la recta r ≡ 2x+3y-8=0 según la dirección del vector V(8,5). Pasos a seguir: 1.- Calculamos la ecuación de la recta s ≡5x-8y+20=0 que pasa por P y tiene la dirección del vector V(8,5). 2.-Obtenemos Q(-0.87,1,95) como intersección de r y s obtenida en el apartado anterior. 3.- Calculamos P'(-5.75,-1.09) considerando Q como punto medio del segmento PP'. P '(2·p.x-q.x,2·p.y-q.y) = (-5.75,-1.09). 4.- Calculamos el simétrico ortogonal de P' respecto de r, siguiendo las instrucciones del apartado 2, y obtenemos P"(2.30,7.52). Si atendemos al gráfico podemos observar que podemos modificar la ecuación de la recta r ≡ Ax+By+C=0 , las coordenadas del punto P(p.x, p.y) y las coordenadas del vector V(v1,v2) o gráficamente moviendo el punto P.
|
|
Ejercicio 4.-
a) Calcula la proyección, simétrico y reflejado del punto P(-2,6)respecto de la recta r ≡ -3x+6y-5=0 según la dirección del vector V(-2,3).
b)¿Qué crees que pasaría si la dirección del vector V es perpendicular a la recta r ?. ¿Qué punto crees que coincidiría con P, su proyección o su reflejado?. ¿ Sabrías calcular mentalmente el simétrico y reflejado del punto (0,5) respecto del eje OX según la dirección del eje OY (V= (0,1))?. ¿Y respecto del eje OY según la dirección del eje OX ( V=(1,0))?.
c) Calcula el simétrico y reflejado del punto P (4,5) respecto de la recta r ≡ 2x+5y-8=0 según la dirección del vector V(2,5).
d) ¿Qué pasaría si la recta r tuviese la misma dirección del vector V?. Calcula el simétrico y reflejado del punto P (4,5) respecto de la recta r ≡ 2x+5y-8=0 según la dirección del vector V(-5,2).
e) Calcula el simétrico y reflejado del punto P (1,2) respecto de la recta r ≡ x-5=0 según la dirección del eje OY?.
f) ¿ Qué pasaría si el punto P perteneciese a la recta r?. Calcula el simétrico y reflejado del punto P (4,5) respecto de la recta r ≡ 2x-y -3=0 según la dirección de la bisectriz del primer y tercer cuadrante ( V=(1,1))?.
|
|||||||||||||||
![]()
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.