
 |
¿ LOGARITMOS ? |
| 4º ESO Opción B | |
Las actividades a realizar han de combinar el cuaderno de trabajo con el ordenador y/o con la calculadora:
| ACTIVIDAD 13 PROPIEDADES DE LOS LOGARÍTMOS. UN POCO DE HISTORIA |
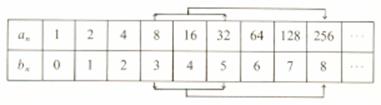
Compara estas dos progresiones:
1, 2, 4, 8, 16, 32, 64, 128, 256, ....................
0, 1, 2, 3, 4, 5, 6, 7, 8, ......................
La primera es geométrica de razón 2, y la segunda aritmética de diferencia 1. Además, la segunda es la sucesión de los exponentes de los términos de la primera, expresados éstos como potencias de 2:
|
1 = 2 |
2 = 2 |
4 = 2 |
8 = 2 |
16 =
2 |
32 =
2 |
............... |
|
0 |
1 |
2 |
3 |
4 |
5 |
............. |
Luego
cada término de la segunda sucesión se obtiene calculando el log![]() del correspondiente término de la
primera:
del correspondiente término de la
primera:
3
= log![]() 8
; 5 =
log
8
; 5 =
log![]() 32 ;8 =
log
32 ;8 =
log![]() 256
256
1 2 4 8 16 32 64 ..... x
0
1 2 3 4 5 6 ......
log![]() x
x
Observa que la suma en la progresión aritmética corresponde al producto en la geométrica:
8 . 32 = 256 ![]() a
a
![]() .
a
.
a![]() = a
= a![]() en
la progresión geométrica
en
la progresión geométrica
3 + 5 =
8 ![]() b
b
![]() +
b
+
b![]() = b
= b![]() en la
progresión aritmética
en la
progresión aritmética
Expresamos este resultado mediante logaritmos: 3 + 5 = 8
![]() log
log![]() 8
+ log
8
+ log![]() 32
= log
32
= log![]() (8.32)
(8.32)
a) Comprueba de igual manera que la sustracción en la progresión aritmética corresponde a la división en la geométrica.
b) ¿Son ciertas las igualdades siguientes? ¿Por qué?
log![]() 16 +log
16 +log![]() 8= log
8= log![]() (16 . 8) ; log
(16 . 8) ; log![]() 16 ‑ log
16 ‑ log![]() 8= log
8= log![]()
![]() ;
log
;
log![]() 16
16![]() = 2 log
= 2 log![]() 16 ; log
16 ; log![]()
![]() =(1/3) log
=(1/3) log![]() 64
64
La gran ventaja del cálculo con logaritmos es la posibilidad de rebajar el grado de las operaciones aritméticas. Acabas de ver que transforman los productos en sumas, los cocientes en restas, las potencias en multiplicaciones y las raíces en divisiones por el índice de la raíz.
Desde la antigüedad,
diversos matemáticos trabajaron e investigaron en este campo. Arquímedes(siglo
III) comparó y estudió las dos progresiones que has visto anteriormente, pero
fue Stifel (siglo XVI) quien sacó consecuencias importantes sobre ellas. La
generalización de estos resultados a cualquier razón la progresión geométrica,
no sólo a 2, llegaría años más tarde de manos de Bürgl y Napier (siglo XVII).
Estos construyen y perfeccionan tablas en las
que aparecen diversos logaritmos, sin hablar de una base para ellos, aunque
ambos se aproximan al número e como base (los logaritmos con base e se llamaron
logaritmos neperianos,en honor a Napier y se representan como ln x en lugar de log![]() x).
x).
Posteriormente, Briggs,
amigo de Napier, recogiendo las ideas de éste, construyó unas nuevas tablas
logaritmos con base el número 10. Los logaritmos con base 10 se llamaron
decimales, pues el 10 es la base de nuestro sistema decimal de numeración. Igual
que en el caso de los logaritmos neperianos, su notación se abrevia, suprimiendo
en este caso el 10 al escribirlos: log ![]() x = log x.
x = log x.
Inmediatamente después se mejoraron las tablas, pasando de calcular logaritmos con catorce cifras decimales a las actuales, en las que aparecen de cuatro a cinco cifras decimales. Con las calculadoras científicas, provistas de las teclas log y ln no es necesario utilizar las tablas.
|
La gran ventaja de los logaritmos consiste en que crecen mucho más despacio que los propios números.
En base 10,
por ejemplo, mientras x recorre desde 1 hasta un billón (=10
Recuerda
ln x
= log |
| ACTIVIDAD 14 EL OIDO HUMANO |
El oído
humano percibe un rango enorme de intensidades sonoras I (medidas en vatios/m![]() ), entre un umbral I
), entre un umbral I![]() = 10
= 10![]() y sonidos del orden de billones de veces más intensos,
como muestra la siguiente tabla:
y sonidos del orden de billones de veces más intensos,
como muestra la siguiente tabla:
|
Intensidad aproximada de algunos sonidos |
Vatios/m |
db |
|
Umbral de audición |
10 |
0 |
|
Susurros |
5.10
|
27 |
|
Conversación normal |
3.10 |
65 |
|
Tráfico muy intenso |
8.10 |
89 |
|
Martillo neumático |
3.10 |
95 |
|
Umbral del dolor |
10 |
120 |
|
Reactor (poscombustíón) |
8.10 |
149 |
Pero al crecer la intensidad geométricamente, la sensación percibida lo hace de forma aproximadamente aritmética. Por eso se introdujo la escala de medida en belios y decibelios (en honor de A. G. Bell, el inventor del teléfono), en la cual un sonido de intensidad I tiene, por definición, un nivel de intensidad de
D = 10 log ![]() decibelios. Así, el sonido umbral
decibelios. Así, el sonido umbral ![]() corresponde a 0 decibelios y un tráfico muy intenso a
corresponde a 0 decibelios y un tráfico muy intenso a
D=10 log![]() =10log
=10log 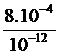 =10log(8.10
=10log(8.10![]() )=10(log8+8)=10(0,9+8)=89decibelios
)=10(log8+8)=10(0,9+8)=89decibelios
Aplicación: Calcula el nivel en decibelios de cada apartado de la tabla anterior y comprueba tus resultados.
| ACTIVIDAD 15 UN TERREMOTO DE 6.7 EN LA ESCALA RITCHER |
El 28 de julio de 1976, a las tres de la madrugada, un terremoto de magnitud 7,9 arrasó la ciudad china de Tanghan ,
cerca de Beijing, causando 600.000 muertos. El 28 de diciembre de 1908, uno de magnitud 7,5 mataba en Messina (Italia)
a 120.000 personas. El 30 de septiembre de 1993, uno de magnitud 6,4 causó miles de víctimas en la India. Pero ¿que
significa «magnitud»?
Una primera medida de la intensidad de los terremotos son los daños que ocasiona. Para lograr una caracterización más precisa, se han desarrollado diversas escalas. Ahora bien, hay una dificultad: parece lógico medir los seismos por la energía que liberan, pero estas energías son números muy enormes en ocasiones. Baste decir que hay terremotos cien mil millones de veces más fuertes que otros, y por otro lado que uno no muy intenso (magnitud 5,5) libera tanta energía como la explosión nuclear de 10 kilotones realizada en Bikini en 1946.
Para evitar esos números tan grandes, igual que ocurre para medir los sonidos, las escalas usan logaritmos. La escala más utilizada la introdujo en 1935 C. Richter (1900‑1985) y define la magnitud M de un terremoto en función de la amplitud A de sus ondas superficiales así:
M = log A + C (donde C = 3,3 + 1,66 log D ‑ log T es una
constante que depende del período T de las ondas registradas en el sismógrafo y
de la distancia D de éste al epicentro, en grados angulares). Es muy
importante darse cuenta de que la magnitud M es una medida logarítmica. Eso hace
que la diferencia entre dos seismos de magnitudes M![]() =
6 y M
=
6 y M![]() =
8, que dicho así no parece muy grande, significa en realidad que en un caso log ( A
=
8, que dicho así no parece muy grande, significa en realidad que en un caso log ( A![]() )+
C = 6, y en el otro log (A
)+
C = 6, y en el otro log (A![]() )
+ C = 8.
)
+ C = 8.
Restando vemos que logA![]() ‑
logA
‑
logA![]() =
2, o sea log (A
=
2, o sea log (A![]() /
A
/
A![]() ) =
2, de donde A
) =
2, de donde A![]() =
100A
=
100A![]() ¡100 veces más intenso!
¡100 veces más intenso!
Al ser logarítmica la magnitud M, una diferencia de 1 unidad en magnitud significa 10 veces más de amplitud en la onda sísmica registrada, lo cual puede ser catastrófico en sus efectos. Un terremoto de magnitud 1 o 2 es muy débil, y los de magnitud mayor que 7 devastadores. El más fuerte registrado en España tuvo lugar en Granada en 1884,con una magnitud 6,7 en la escala Richter. El de San Francisco de 1906 tuvo magnitud 8,25.
Aplicación: Investiga y contesta a éstas cuestiones:
¿Que intensidad tuvo el terremoto que provocó el "tsunami" del 26 de Diciembre del año 2004
en el Sudeste Asiático?
El posterior terremoto de intensidad 8,7 ¿en que lugar sucedió?¿en que fecha?.
|
|
|
|||
| Miguel Ángel Cabrerizo Romero | |
 |
|
| Ministerio de Educación, Cultura y Deporte. Año 2005 |

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.