
 |
MATRICES: OPERACIONES II |
| Álgebra | |
| 7. PRODUCTO DE UNA MATRIZ FILA POR UNA MATRIZ COLUMNA | |
|
En cursos anteriores se ha estudiado el producto escalar de vectores, que en el caso de R2, se definía de la forma siguiente: Si u = (a , b) y v = (c , d) son dos vectores, su producto escalar es: u . v = a . c + b . d. De forma análoga, se puede definir el producto de una matriz fila por una matriz columna: |
|
|
|
Es evidente que el número de elementos de la matriz fila tiene que ser igual al número de elementos de la matriz columna |
| 8. PRODUCTO DE MATRICES | |
|
El producto de matrices no está definido en todos los casos. Para que dos matrices se puedan multiplicar es necesario que el número de columnas de la primera matriz coincida con el número de filas de la segunda matriz, es decir, si la matriz A = ( aij ) tiene dimensión m x n y la matriz B = ( bij ) tiene dimensión p x q, para que se pueda efectuar el producto A . B es necesario que n = p. Por otra parte, la matriz producto P = ( pij ) tendrá por dimensión m x q, es decir, el número de filas de la matriz A y el número de columnas de la matriz B. Cada elemento pij de la matriz P se obtiene multiplicando la fila i de la matriz A por la columna j de la matriz B, siguiendo el procedimiento descrito en el punto anterior. |
|
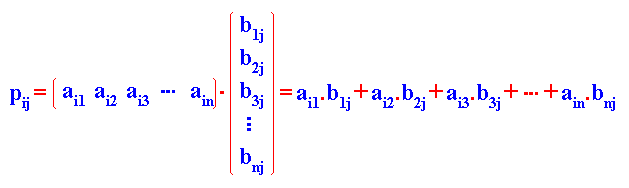 |
|
 |
|
PROPIEDADES DEL PRODUCTO DE MATRICES Sean A, B Y C matrices. Siempre que sea posible efectuar los productos indicados, de acuerdo con la condición anterior, se verifica: 1ª Asociativa: ( A . B) . C = A . ( B . C ) 2ª Elemento neutro: I ( matriz identidad o unidad ) A . I = I . A = A 3ª Distributiva respecto de la suma de matrices: A . ( B + C ) = A . B + A . C 4ª El producto de matrices no es, en general, conmutativo: A . B ≠ B . A 5ª Matriz Inversa: Dada una matriz cuadrada A, si existe otra matriz B que verifique A . B = B . A = I (matriz identidad), entonces se dice que B es la matriz inversa de A y se representa por A-1. ( A . A-1 = A-1 . A = I ) |
| Alfredo Pena Iglesias | ||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2006 | ||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.