

|
representación de funciones polinómicas y racionales |
I. Representación de funciones polinómicas conocidos sus coeficientes.
En esta primera escena se pretenden tr es objetivos:
Representar funciones conocidos los coeficientes de sus diversos términos.
Conocer cómo varían dichas representaciones al modificar algunos de los coeficientes.
Observar en cuántos puntos puede cortar la función al eje de abscisas, OX, dependiendo de su grado.
NOTAS de uso para alumnos sin experiencia con Descartes.
- En la zona norte de la escena se dispone de los controles:
zoom: permite acercar o alejar el conjunto de la escena.
Escala OX y Escala Oy: permiten modificar, independientemente, la escala de cada eje.
O.x, O.y: permiten trasladar el origen de coodenadas.
decimales: indica el número de cifras decimales con que se desea trabajar ( 0 y 1).
- En la zona sur de la escena se dispone de los controles:
x5, x4, x3, x2, x1 y x0:indican los coeficientes de los términos de los diversos grados.(Consideramos hasta grado 5, porque permite suficiente generalidad).
relleno(s/n): permite colorear los intervalos en los que la función es positiva o negativa.
- Modo de escribir funciones: la función y=4*(x^5)-3*(x^3)+2*(x^2)-1*(x^1)-6 corresponde a:
ACTIVIDADES
1.- Familiarízate con los controles: durante unos 5 minutos manipúlalos hasta que entiendas su funcionamiento.
2.- Representa las funciones que creas oportunas. Duración: unos 10 minutos.
3.- Representa funciones siguiendo la pauta:
a) Antes de cada uno de los siguientes ejercicios, pon todos los coeficientes en 0.
b) Modifica sólo x0. Aparecen rectas horizontales.
c) Modifica x1: aparecen rectas que pasan por el origen. Modifica luego x2: las rectas se desplazan.
d) Modifica x2: parábolas cuyo vértice coincide con el origen. Modifica x1. Modifica x0. Observa qué ocurre.
e) Modifica x3: a partir de ahora llamaremos curvas a las gráficas. Modifica x1. Modifica x2. Modifica x0. Observa.
f) Modifica x3. Modifica x2. Modifica x1. Modifica x0. Observa y anota en tu cuaderno.
Fíjate en las secuencias que te indico. No las varíes: se pretende que veas el efecto de modificar cada uno de los coeficientes. Si quieres, al final, puedes modificar lo que quieras y como quieras.
4.- Representa funciones, pero siguiendo la siguiente pauta:
a) Modifica x4. Modifica x2. Modifica x3. Modifica x1.Modifica x0. Observa y anota en tu cuaderno.
b) Modifica x4. Modifica x3. Modifica x2. Modifica x1.Modifica x0. Observa y anota en tu cuaderno.
c) Modifica x5. Modifica x3. Modifica x1. Modifica x4.Modifica x2.Modifica x0. Observa y anota en tu cuaderno.
d) Modifica x5. Modifica x4. Modifica x3. Modifica x2.Modifica x1.Modifica x0. Observa y anota en tu cuaderno.
5.- Se pretende averiguar cuántos puntos de corte con el eje OX puede tener una función, dependiendo de su grado. Por ejemplo: si queremos hallar si es posible que una función de tercer grado tenga 0, 1, 2, 3, 4 ... puntos de corte con el eje de abscisas, pues manipulamos los controles, observamos los puntos de corte de las distintas curvas y anotamos los resultados obtenidos.
¡ No queremos el valor máximo de puntos de corte, sino todos los valores posibles !
Puedes rellenar una tabla como ésta:
Ejemplos Puntos de corte posibles Función de grado 1 Función de grado 2 y=x^2+4, y=x^2, y=x^2-4, 0, 1, 2 Función de grado 3 Función de grado 4 Función de grado 5
6.- Resuelve las ecuaciones, y = 0, de la tabla anterior. (Gráfica y analíticamente).
7.- Resuelve las inecuaciones: y >= 0, y > 0, y < 0, y <= 0, de la tabla anterior.(Gráfica y analíticamente). Puedes ayudarte del control relleno.
II. Representación de funciones polinómicas conocidos sus ceros.
En esta primera escena se pretenden tres objetivos:
Representar funciones conocidos sus ceros.
Conocer cómo varían dichas representaciones al modificar algunos de los ceros.
Observar en qué puntos corta la función al eje de abscisas, OX.
NOTAS de uso para alumnos sin experiencia con Descartes.
- En la zona norte de la escena se dispone de los mismos controles que en la escena anterior.
- En la zona sur de la escena se dispone de los controles:
A: es el coeficiente del término de mayor grado.
r1, r2, r3 y r4:indican las raíces de la función.(Consideramos hasta 4 raíces, lo que permite suficiente generalidad).
relleno(s/n): permite colorear los intervalos en los que la función es positiva o negativa.
- Modo de escribir funciones: la función que consideramos es y=A*(x-r1)*(x-r2)*(x-r3)*(x-r4). Hay que tener en cuenta que sólo se evalúan el número de raíces que indicamos en nº de raíces, en el orden r1, r2, r3 y r4. Las demás, aunque se indiquen, no se evalúan.
ACTIVIDADES
8.- Familiarízate con los controles: durante unos 5 minutos manipúlalos hasta que entiendas su funcionamiento.
9.- Representa funciones con las raíces que te parezcan oportunas. Duración: unos 10 minutos.
10.- Se pretende averiguar el número máximo de puntos de corte con el eje OX que puede tener una función, dependiendo de su grado y relacionarlo con su número de raíces.
¡ Ahora sí queremos el número máximo de puntos de corte !
Puedes rellenar una tabla como ésta:
Ejemplos Puntos de corte (máximo) Función de grado 1 Función de grado 2 y=(x-3)*(x+2), y=2x(x-4) 2 Función de grado 3 Función de grado 4 Función de grado 5
11.- Resuelve las ecuaciones, y = 0, de la tabla anterior. (Gráfica y analíticamente).
12.- Resuelve las inecuaciones: y >= 0, y > 0, y < 0, y <= 0, de la tabla anterior.(Gráfica y analíticamente). Puedes ayudarte del control relleno.
III. Representación de funciones racionales conocidos sus ceros.
En esta primera escena se pretenden tres objetivos:
Representar funciones racionales conocidos sus ceros.
Conocer cómo varían dichas representaciones al modificar algunos de los ceros.
Observar en qué puntos corta la función al eje de abscisas, OX, y en cuáles tiene asíntotas.
NOTAS de uso para alumnos sin experiencia con Descartes.
- En la zona norte de la escena se dispone de los mismos controles que en la escena anterior.
- En la zona sur de la escena se dispone de los controles:
nº r.n: número de raíces del numerador que deseamos.
nº r.d: número de raíces del denominador.
A: es el coeficiente del término de mayor grado.
r1, r2: indican las raíces del numerador de la función racional.
r3 y r4:indican las raíces del denominador de la función.
(Consideramos que esto permite suficiente generalidad).
relleno(s/n): permite colorear los intervalos en los que la función es positiva o negativa.
- Modo de escribir funciones:
Hay que tener en cuenta que sólo se evalúan el número de raíces que indicamos en nºr.n y nºr.d, en el orden r1y r2 en el numerador y r3 y r4 en el denominador. Las demás, aunque se indiquen, no se evalúan.
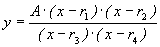
ACTIVIDADES
13.- Familiarízate con los controles: durante unos 5 minutos manipúlalos hasta que entiendas su funcionamiento.
14.- Representa funciones con las raíces que te parezcan oportunas. Duración: unos 10 minutos.
15.- Se pretende que relaciones las raíces del numerador con los puntos de corte con el eje OX y que relaciones las raíces del denominador con las asíntotas: esas rectas verticales a las que la curva se aproxima.
Puedes rellenar una tabla como ésta y copiar en ella algunas de las funciones que has representado y las observaciones que has hecho.
Función
Raíces del
numerador
Puntos de corte
con el eje OX
Raíces del
denominador
Asíntotas
16.- Resuelve las ecuaciones, y = 0, de la tabla anterior. (Gráfica y analíticamente).
17.- Resuelve las inecuaciones: y >= 0, y > 0, y < 0, y <= 0, de la tabla anterior.(Gráfica y analíticamente). Puedes ayudarte del control relleno.
18.- Una última propuesta: pon como raíces del numerador 1 y 2, y como raíces del denominador 2 y 3. ¿ Qué pasa en x=2 ?. ¿ No pasa nada ?. ¿ Falla algo?. Bueno, esto quizás debieras preguntárselo a tu Profesor@, no sé si ahora, en 4º E.S.O. o en 1º de Bachillerato.
III. Conclusión.
En esta primera práctica el alumno debe:
- conocer la representación de funciones polinómicas y racionales. Prestará especial atención al hecho de que los puntos de corte con el eje de abscisa y las asíntotas, son puntos en los que, es posible, que la función cambie de signo: sólo se asegura esa posibilidad, no hay certeza. Esto ayuda a representar funciones.
- comprender que el número máximo de puntos de corte con el eje OX de una función coincide con su grado. Que en caso de "faltarle" le faltan por pares. Que lo anterior en nada contradice la existencia de raíces múltiples. Que de lo que hablamos es, en definitiva, del "punto de vista gráfico" del Teorema Fundamental del Álgebra.
- saber resolver ecuaciones e inecuaciones a partir de la gráfica de una función.
|
|||||||||||