
Análisis
 |
Familias
de funciones
|
|
Análisis |
FUNCIONES LINEALES
1. Un determinado medicamento tiene como dosis 2 mg por kilogramo de peso del paciente.
a. Establece la relación entre los miligramos de la dosis y el peso del paciente.
b. Haz una gráfica.
Nota: Si tienes dudas puedes ayudarte del siguiente applet:
Introduciendo el peso obtienes los mg de medicamento que hay que administrar.
Arrastrando el control se observa la relación entre el peso y los mg de medicamento.
c. Si administramos 32 mg de medicamento, ¿cuánto pesa el paciente?. Ayúdate del applet para contestar a la pregunta y luego justifica algebraicamente la respuesta.
2. Un recibo de luz refleja los siguientes conceptos: una cantidad fija por potencia contratada y una cantidad variable por consumo. La cuota fija es de 10€ y 0,082 por Kw-hora.
a. ¿Cómo expresarías el coste del recibo de la luz en función del número de kw-hora consumidos?.
b. ¿Cuál es el recibo para un consumo de 100 K-hora?.
c. Si la factura de la luz es de 40€ ¿cuántos Kw-hora se han consumido?.
Nota: Puedes ayudarte del siguiente applet:
Definición: Toda relación funcional de la forma y=a·x o y=a·x+b, donde a y b son números reales, se llama funciones lineales.
La representación gráfica de dichas funciones es una recta.
Las relaciones que describen los ejercicios 1 y 2 (y=2·x, y=0,08·x+10) son funciones lineales.
Pendiente y ordenada en el origen: en la expresión algebraica de la función lineal y=a·x+b veamos el significado de los coeficientes a y b:
Observa el siguiente applet:
* ¿Cuál es la expresión algebraica de la recta que muestra el applet al inicio?
Ordenada en el origen:
Si x=0, cuál es el valor de la ordenada (y=...). En la expresión general de la recta y=a·x+b si la abscisa es cero (x=0), cuál es el valor de la ordenada (y=...).
Al valor b de la ecuación se le llama ordenada en el origen.
Varía en el applet el valor de b y observa. ¿Gráficamente qué representa la ordenada en el origen?.
Si b=0, la recta pasa por el ... ... ... de coordenadas (compruébalo con el applet). En este caso la expresión algebraica de la recta es y=a·x (función de proporcionalidad directa).
Pendiente de la recta:
Varía en el applet el valor de la a, cuanto mayor es este valor, ¿cómo es la inclinación de la recta?.
Al valor de a se le llama pendiente de la recta.
Si a>0 la recta es creciente pues a valores mayores de la abscisa (x), le corresponden valores mayores de la ordenada (y). Es decir a originales mayores corresponden originales mayores.
Comprueba esta afirmación arrastrando el punto P sobre la recta.
Si a<0 la recta es ... ... ... ... pues a valores mayores de la abscisa (x), le corresponden valores ... ... ... ... de la ordenada (y). Es decir a originales mayores corresponden originales mayores.
Usa el applet para obtener varias rectas decrecientes.
¿Cómo debe ser la pendiente de la recta para que esta ser horizontal?. Usa el applet para obtener varias rectas horizontales. ¿Cuál es la expresión algebraica de este tipo de rectas?.
Ejercicios:
1. Dibuja en tu cuaderno las rectas de ecuación (sin realizar una tabla de valores), comprueba que están bien utilizando el applet:
a. y=3x b. y=-3x c. y=3x-2 d. y=3x+2 e. y=-3/2x+1 f. y=-2 g. x=3
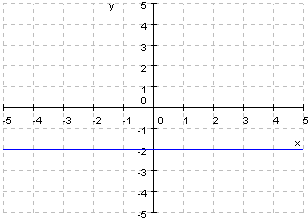
2. Dadas las siguientes gráficas:
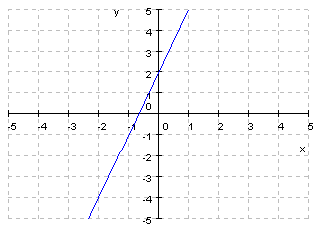 |
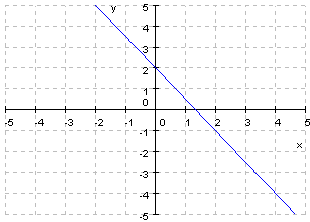 |
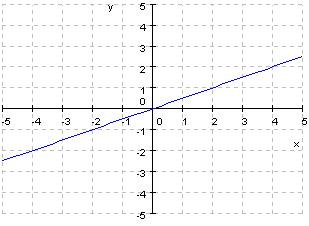 |
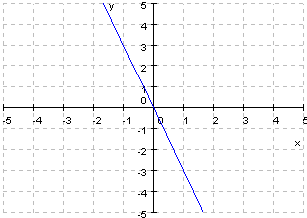 |
 |
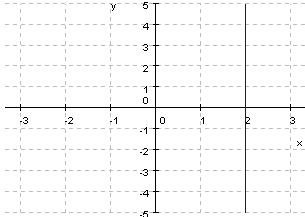 |
a. ¿Cuales son de proporcionalidad inversa?
b. Obtener las pendientes y ordenas en el origen
c. Dar su expresión algebraica.
d. Comprobar que están bien utiliza el applet.
e. Cuales son crecientes y cuales decrecientes
1. Queremos construir un rectángulo de 20 cm de perímetro.
a. Dibuja una gráfica que refleje cómo varía la altura dependiendo de la base.
b. Escribe la relación entre la base y la altura.
c. Comprueba el dibujo de la gráfica utilizando el applet.
| Gabriel Sosa Felipe | ||
 |
||
| Ministerio Educación. Año 2004 | ||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.