|
Ecuación es una igualdad literal que sólo es cierta para algunos valores de
las letras.
La letra o letras desconocidas de una ecuación se llaman
incógnitas. En la
ecuación x + 2 = 9 la incógnita es x. La incógnita de una ecuación se puede designar
con cualquier letra, pero en general se utiliza la letra x
Soluciones de una ecuación son los números que la verifican, es decir, los
números que convierten la ecuación en una igualdad de números cierta.
Resolver una ecuación es hallar sus soluciones
Así la ecuación x + 4 = 12 sólo se verifica si
x = 8. Se dice que 8 es la solución de la ecuación
|
|
Términos de una ecuación son los sumandos que tienen cada miembro de la
ecuación, pueden ser términos en x, y términos independientes
Por ejemplo la ecuación:
3x - 1 = x + 3
Primer miembro:
3x - 1
Segundo miembro:
x + 3
Términos en x:
3x, x
Términos independientes: -1,
3
Transposición de términos: Pasar términos de un miembro a otro de una
igualdad según las siguientes reglas:
El término
que está sumando en un miembro, pasa al otro restando, y viceversa. Si está
multiplicando, pasa al otro miembro dividiendo, o viceversa. Ej:
|
|
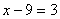
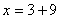
|
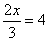
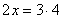
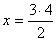
|
|
ECUACIONES DE LA FORMA a x + b = c , con a#0
|
|
Para resolver la ecuación: 2x + 7 = 13
1) Se deja el término en x en el primer miembro y
los términos independientes se pasan al segundo miembro: 2x = 13 - 7
2) Se reducen los términos semejantes: 2x = 6
3) Se despeja la incógnita: x = 6/2
x=3
|
|
|
En la escena adjunta, asigna a las
letras los valores correspondientes para cada ecuación, lo puedes realizar:
Con las flechas o con el teclado |
|
Resuelve las siguientes ecuaciones en tu
cuaderno de trabajo y comprueba cómo lo hace la escena: |
|
|
|
|
a) 2x + 8 = 18 |
b) 3x - 7 = 13 |
c) 4x - 12 = 8 |
d) -5x -20 = 10 |
|
e) 8x - 40 = 0 |
f) - 4x + 30 = 18 |
g) 3x - 6 = 0 |
h) - 3x - 2 = 4 |
|
ECUACIONES DE LA FORMA ax + b = cx + d
|
|
Para resolver esta ecuación 6 x - 4 = 3x + 2
1) Se pasan todos los términos en
x a uno de los miembros de la
ecuación, por ejemplo al primero y se pasan los términos independientes al
segundo miembro: 6x - 3x = 2 + 4
2) Se reducen los términos semejantes: 3x = 6
3) Se despeja la incógnita
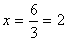
|
|
|
Resolver las ecuaciones siguientes:
a) 2x - 3 = 4x - 7 |
b) 5x + 4 = 6x + 3 |
c) 6x - 1 = 8x - 5 |
d) 3x + 10 = 5x - 6 |
|
e) 4x + 1 = 9x - 64 |
f) 7x + 6 = 9x - 2 |
g) - 3x + 2 = x + 10 |
h) -6x + 3 = - 2x + 1 |
|
ECUACIONES CON PARÉNTESIS
|
|
Para resolver esta ecuación
2(7 - x) + 7x = 8 - 5(x - 1) + 8x + 4
1) Se suprimen los paréntesis aplicando la propiedad distributiva
14 - 2x + 7x = 8 - 5x + 5 + 8x + 4
2) Se trasponen los términos (los términos en x al primer miembro y los
términos independientes al segundo):
-2x + 7x + 5x - 8x = 8 + 5 + 4 - 14
3) Se reducen los términos semejantes:
2x = 3
4) Se despeja la incógnita:
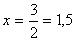
|
|
|
Resuelve las ecuaciones:
a) 3 (x + 6) = 2 ( x - 5) |
b) 9 (x - 1) = 6 (x + 3) |
c) 8 (x -
2) = 12 (x - 3) |
d) 6 (- x + 8) = 7 ( x - 1) |
|
|
|
|
|
|
e) - 3 ( 2x + 5) = - 4 ( -x + 2) |
f) 5 ( -2x + 6) = - 3 ( -x + 3) |
g) - 2 ( x + 7) = 2 ( 3x + 9) |
h) - 4(3x - 5) = -2 (x - 8) |
|
|
|
|
|
|
ECUACIONES CON DENOMINADORES
|
|
Para resolver esta ecuación:
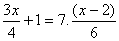
1) Se reduce a común denominador, calculando el mínimo común múltiplo de los
denominadores
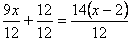
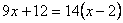
2) Se suprimen los paréntesis
aplicando la propiedad distributiva:
9x + 12 = 14x - 28
3) Se trasponen términos (los
términos en x a un miembro y los términos independientes al otro)
9x - 14x = -28 - 12
4) Se reducen términos semejantes:
-5x = -40
5)
Se despeja la incógnita:
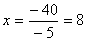
|
|
|
Resuelve las siguientes ecuaciones: |
|
a) |
b) |
c) |
d) |
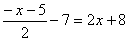 |
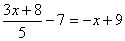 |
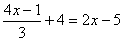 |
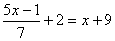
|
|
|
|
|
|
|
|
|
|
|
|
e) |
f) |
g) |
h) |
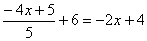 |
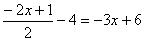 |
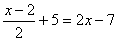 |
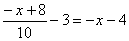 |
|
|
|
|
|
Blanca Barroso González |
| |
 |
|
|
|
|
 |

