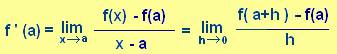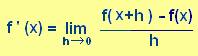|
DERIVADA
D'UNA FUNCIÓ EN UN PUNT FUNCIÓ
DERIVADA |
En aquesta pràctica
intentarem entendre el concepte de derivada d'una funció en un punt i de la
funció derivada. Llegeix els apartats atentament i segueix les indicacions que
se't van donant. Prepara paper i bolígraf per fer els exercicis i respondre a
les preguntes.
I.
TAXA DE VARIACIÓ MITJANA
La Taxa de Variació Mitjana (TVM) d'una
funció f(x) en un interval [ a,b ] és el quocient entre l'increment de la
funció i l'increment de la variable x en aquest interval:
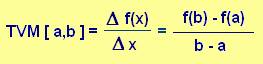
Observa la següent escena en la que hi
ha representada una funció i dos punts A i B d'aquesta funció.
COMPROVA:
|
|
a)
Mou els punts A i B per sobre la funció fent un clic directament sobre ells.
També els pots moure amb els controls de la part inferior de l'escena.
Comprova que les coordenades escrites a la part superior esquerra de l'escena
són correctes. b)
Posa el control "Visualitza"
igual a 1 i comprova els valors que va prenent l'increment de la funció
en l'intèrval quan mous els punts. Observa que aquest increment és igual a la
longitud del segment blau. c)
Posa el control "Visualitza"
igual a 2 i comprova els valors que va prenent l'increment de la variable
x en l'intèrval quan mous els punts. Comprova que aquest increment és igual a
la longitud del segment verd. d)
Posa el control "Visualitza"
igual a 3 i comprova que el quocient entre els dos increments és
correcte. e) Prem el control "Animació" i comprova que aquests
increments són els catets del triangle i que al dividir-los ens dóna la
tangent de l'angle |
CONCLUSIÓ:
El
quocient entre els increments és igual a la tangent de l'angle, que també és
igual al pendent de la recta vermella que uneix els dos punts. Aquesta recta ÉS LA RECTA SECANT a la funció en els
dos punts A i B.
LA TAXA DE VARIACIÓ
MITJA D'UNA FUNCIÓ ENTRE DOS PUNTS ÉS IGUAL AL PENDENT DE LA RECTA SECANT A LA
FUNCIÓ EN AQUESTS DOS PUNTS
II.
TAXA DE VARIACIÓ INSTANTÀNIA. CONCEPTE DE DERIVADA
La
Taxa de Variació Instantània (TVI) és el límit de la taxa de variació mitja
quan l'intèrval tendeix a zero, és a dir, quan en l'intèrval [ x,a ] el punt
"x" va acostant-se infinitament a "a":

COMPROVA:
|
|
a)
Mou el punt A o B a la posició que vulguis. Amb els controls inferiors ves acostant
el punt A al B o viceversa. Observa que quan un punt s'acosta a l'altre, en
el límit, els dos punts coincideixen, són un de sol. En aquest moment la
recta secant es converteix en la recta tangent a la funció. b)
Fes aquesta aproximació, aquest "pas
al límit", en diferents punts. CONCLUSIÓ: La Taxa de Variació Instantània d'una funció
en un punt és igual a la derivada de la funció en aquest punt. Aquí tenim
dues expressions anàlogues de la definició de derivada:
|
LA DERIVADA D'UNA
FUNCIÓ EN UN PUNT ÉS IGUAL AL PENDENT DE LA RECTA TANGENT A LA FUNCIÓ EN AQUEST
PUNT
III.
DERIVADA D'UNA FUNCIÓ EN UN PUNT. FUNCIÓ DERIVADA
Així
doncs, el pendent de la recta tangent a la funció en un punt és igual a la
derivada de la funció en aquest punt. En la següent escena pots veure un punt A
de la funció i la recta tangent a la funció en aquest punt A
COMPROVA:
|
|
a)
Mou el punt A a la posició que vulguis i comprova que la recta dibuixada és
sempre la tangent a la funció en cada punt. b)
Mou el punt A a la posició que vulguis i observa el valor del pendent (m) que
apareix a la part inferior. c)
Observa el punt P (en blau). És un punt que té per abcisa la mateixa que el
punt A i per ordenada el valor del pendent de la recta tangent. d)
Posa el control "F.derivada"
igual a 1 i mou el punt A. El conjunt de tots els punts que tenen com a
ordenada el valor de la derivada en cada punt ÉS LA FUNCIÓ DERIVADA. CONCLUSIÓ: L'expressió
matemàtica de la definició de funció derivada és:
|
LA DERIVADA f'(x) D'UNA FUNCIÓ f(x) ÉS EL
CONJUNT DELS PUNTS QUE EN CADA ABCISA TENEN L'ORDENADA IGUAL AL VALOR DEL
PENDENT DE LA RECTA TANGENT A LA FUNCIÓ f(x).
![]()
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.