CÓNICAS

2. LA ELIPSE

I. ELIPSE..

Una elipse es una curva cerrada que se obtiene como intersección de un cono circular recto y de un plano no paralelo a su base, el eje o algún elemento del cono.

Supondremos que a es estrictamente mayor que b, ya que en caso contrario, o se trata de una circunferencia (si a = b) o de otra elipse de similar estudio.

La fórmula matemática de la elipse, centrada en el origen de coordenadas es

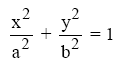
   Los puntos de corte de la elipse y el eje OX (abscisas) son    A(a, 0) y A´(-a, 0)

   El eje mayor es el segmento AA´. El semieje mayor es a.

   Los puntos de corte de la elipse y el eje OY (ordenadas) son  B(0, b) y B´(0, -b).

   El eje menor es el segmento BB´. El semieje menor es b.

   Los puntos F(c, 0) y F´(-c, 0) se llaman focos.

   Para hallar los focos necesitamos conocer un nuevo valor c llamado semidistancia focal, que verifica la siguiente ecuación: c2= a2 - b2.

    Se llama excentricidad al cociente entre c y a. Se denota con la letra e y su valor está entre 0 y 1.

1. Cambia a y b para ver cómo calcular los vértices y los focos de la elipse

2. Dibuja la elipse anterior en tu cuaderno, con todos los elementos que observas.

3. Calcula todos los elementos anteriores si a=4 y b=2. Comprueba que coincide con los valores que se obtienen en la escena anterior.

II. DEFINICIÓN DE ELIPSE

Definición. Una elipse es el lugar geométrico de los puntos cuya suma de distancias a dos puntos fijos llamados focos es constante.

4. Observa cómo cambia la elipse.

5. Cambia los valores de a y b para ver cómo cambia la elipse.

6. Mueve el punto P y comprueba la definición de elipse. Comprueba que efectivamente la suma de distancias de P a los focos F y F´ es constante.

7. Copia la definición de elipse en tu cuaderno.

III. TRAZADO DE LA ELIPSE

En este apartado vamos cómo se puede dibujar una elipse sin ninguna de las definiciones anteriores. De forma muy visual podremos ir cambiando el número de pasos e intuir la gráfica de la elipse.

  1. Dibujamos una circunferencia de centro O y radio a.
  2. Tomamos en su interior un punto cualquiera F’(-c, 0)
  3. Unimos el punto anterior F’ con un punto P de la circunferencia mediante una recta.
  4. Sobre el punto P trazamos la perpendicular a la recta anterior.
  5. Repetimos los pasos 3 y 4 tantas veces como sea posible.

     NOTA: Si tomamos a más pequeño que c, se dibujará la hipérbola

8. Cambia los valores del radio a de la circunferencia y del número de pasos p. Observa cómo se va "dibujando" la elipse.

9. Intenta realizar en tu cuaderno una elipse por este método.

Volver al principio

 

 
  Fco. Javier Payán Jiménez
 
Ministerio de Educación . Año 2005
 
 

 

 

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.