| 1. EL ÁREA BAJO UNA CURVA |
| Dada
una región del plano, su área puede
aproximarse por medio de regiones poligonales inscritas o circunscritas a la misma. Este
procedimiento ya era
conocido por los griegos. Estamos interesados en
calcular el área del recinto amarillo acotado por una línea azul (llamado trapecio
mixtilíneo), limitado por una curva (gráfica de una función continua), el eje de
abscisas y las rectas verticales x=a y x=b, con a y b dos valores reales. Arquímedes
(287-212 a.C.) ya obtuvo resultados importantes como el cálculo del área encerrada por
un segmento parabólico. |
|
|
1.- Observa el siguiente trapecio mixtilíneo. Si tuvieras que elegir un
polígono para aproximar el área del recinto naranja, ¿cuál elegirías?. ¿Por qué?.
| Si aumentas en una
unidad el paso verás una propuesta. |
2.- Analiza las ventajas e inconvenientes
de la
elección de un rectángulo para aproximar el área. Compara con la respuesta de la
actividad 1.
3.- Una vez dado este primer paso ¿Qué harías para
mejorar nuestra primera aproximación?
| Si aumentas
sucesivamente el paso podrás ver una solución. |
|
Cuantos más rectángulos construyamos
mejor será la aproximación. El proceso llevado a cabo es el siguiente:
- Al intervalo [a,b] se le subdivide en subintervalos que
forman las bases de los rectángulos.
- Al realizar la subdivisión del intervalo aparece un
conjunto de números reales ordenados y finito
{x0, x1, x2, x3...,xn} que se llama
partición del segmento [a,b].
- Cada partición compuesta por n+1 puntos determina n
rectángulos. En nuestro caso las bases tienen la misma longitud, aunque en general no es
necesario.
- Se obtienen los rectángulos inscritos dentro del recinto
mixtilíneo, su calculan sus áreas y se obtiene la suma final.
|
|
|
|
6.- Te proponemos otro trapecio mixtilíneo. Repite el proceso y extrae
conclusiones
Se llama suma inferior de Riemann de f asociada a
la partición P={x0, x1, x2, x3...,xn}
a la siguiente expresión
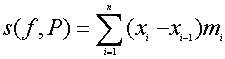
donde mi es el mínimo de los
valores de la función f en el subintervalo [xi-1,xi]. |
|
3. OTRAS
POSIBLES APROXIMACIONES |
| En la actividad 2 se han realizado
aproximaciones de manera que el área obtenida fuese menor que la del recinto mixtilíneo.
Esta no tiene por qué ser la mejor aproximación posible. |
|
|
7.- Deduce otras posibilidades, siguiendo la misma técnica, para aproximar el
área del recinto amarillo, utilizando rectángulos u otras figuras que te parezcan
más adecuadas. Analiza las ventajas e inconvenientes de cada sistema.
| Modificando el
parámetro opción puedes ver dos nuevas propuestas. |
El parámetro paso
nos permite realizar sucesivos refinamientos de la partición. |
Se llama suma superior de Riemann de f asociada a la partición P={x0, x1, x2,
x3...,xn} a la siguiente expresión
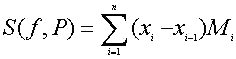
donde Mi es el máximo de los
valores de la función f en el subintervalo [xi-1,xi]. |
|
| 8.- Calcula las sucesivas áreas de las zonas grises para cada
partición. 9.- Escribe como sería
la fórmula general que permita calcular un área mediante la regla de los trapecios
compuesta.
10.- ¿Cuántas veces tendremos que hacer
el proceso para obtener el área del recinto?.
11.- ¿Cómo evolucionan las superficies
grises cuando hacemos más fina la partición?.
12.- Si la base de los rectángulos es
cada vez más pequeña, ¿cómo evolucionarán las sumas superior e inferior de
Riemann?.
|