Máximos y mínimos

	MAXIMA AND MINIMA
	Analysis

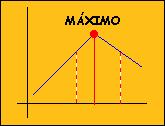
A function y=f(x) reaches a local MAXIMUM at a point x_o when f(x)£f(x_o) in the neighbourhood of x_o
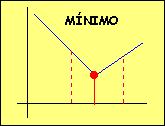
Similarly we can say that it reaches a local MINIMUM at a point x_o when f(x)³f(x_o) in the neighbourhood of x_o

Let's see what happens when we are working with derived functions.

1.Local maxima and minima

2.Calculating maxima and minima

3.Applications

1. LOCAL MAXIMA AND MINIMA

A function y=f(x) reaches a local MAXIMUM at x_o when f(x)£f(x_o) in the neighbourhood of x_o

Change the value of x on the window and check that, in this case, the function INCREASES then DECREASES. Note that the tangent is HORIZONTAL

Therefore:

Similarly y=f(x) reaches a Local MINIMUM at x_o when f(x)³f(x_o) in the neighbourhood of x_o

Now the function first DECREASES then INCREASES. The tangent is also HORIZONTAL.

If a function has a derivative and reaches a maximum or minimum at point x_o, then f'(x_o) = 0

Although this condition is necessary it is not enough as a function could have a derivative of zero at a certain point but not have a maximum or minimum at this point.

Now look carefully at the curves of the function y=f(x),its derivative y=f'(x) and the second derivative y=f''(x) in the window.

As you can see, f reaches a maximum when x=-1 and a minimum when x=1. Change the value of x in the window and look carefully at the values of f' and f'' at these points.

What are the the maximum and minimum values?
What is the relation between the sign of the second derivative and whether f reaches a maximum or minimum?

If f'(x_o) = 0 and f''(x_o) <0, f reaches a maximum at x_o

If f'(x_o)=0 and f''(x_o)>0, f reaches a minimum at x_o

	María José García Cebrian

	Spanish Ministry of Education. Year 2001

Except where otherwise noted, this work is licensed under a Creative Common License