
 |
MÁXIMOS Y MÍNIMOS |
| Análisis | |
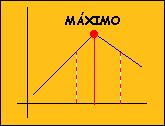
Una función y=f(x) alcanza un MÁXIMO en xo cuando existe un entorno de xo en el que f(x)£f(xo)
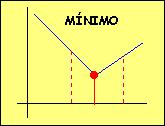
Análogamente diremos que alcanza un MÍNIMO en xo cuando existe un entorno de xo en el que f(x)³f(xo)
 |
 |
Veamos qué ocurre cuando tratamos con funciones derivables.
|
1. MÁXIMOS Y MÍNIMOS RELATIVOS |
||||
|
Una función y=f(x) alcanza un MÁXIMO relativo en xo cuando existe un entorno de xo en el que f(x)£f(xo)
Tenemos
pues que: |
||||
|
Análogamente y=f(x) alcanza un MÍNIMO relativo en xo cuando existe un entorno de xo en el que f(x)³f(xo)
|
||||
|
||||
|
Observa ahora la escena donde están representadas una función y=f(x),su derivada y=f'(x) y la derivada segunda y=f''(x)
|
||||
| María José García Cebrian | ||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2001 | ||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.