Ángulos y rectas paralelas

.

 

1. ÁNGULOS OPUESTOS POR EL VÉRTICE

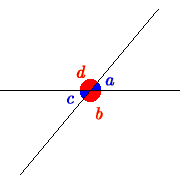
Decimos que dos ángulos son opuestos por el vértice si tienen el mismo vértice y sus lados están en la misma recta.

En la siguiente figura, los ángulos a y c son opuestos por el vértice. Igualmente, los ángulos b y d también lo son. ¿Qué puedes decir de la amplitud de dos ángulos opuestos por el vértice?

  

 

Ejercicio 1.

  • Arrastra el punto P y observa lo que ocurre con la medida de los ángulos opuestos por el vértice marcados.

 

 

2. ÁNGULOS Y RECTAS PARALELAS

Recuerda que una recta que corta a dos ó más rectas del plano recibe el nombre de recta secante. Cuando una recta secante corta a otras dos rectas, aparecen dos tipos de ángulos:

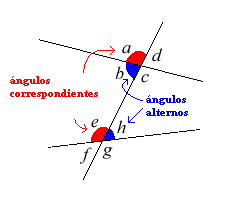
-         Ángulos correspondientes: los ángulos a y e son correspondientes. Además, también  son correspondientes d y h, b y f, c y g.

-         Ángulos alternos: los ángulos b y h son alternos. También lo son los ángulos c y e.

 

Los siguientes ejercicios te servirán para comprobar que los ángulos correspondientes, y los ángulos alternos que se forman al cortar dos rectas paralelas por una secante son iguales.

  

 

 

Ejercicio 2.

Arrastra el punto P hasta construir la recta secante a las dos paralelas deseada. A continuación, mueve el punto Q hasta que los ángulos correspondientes se superpongan. Comprueba así que los ángulos correspondientes son iguales.

  

 

 

Ejercicio 3.

Arrastra el punto P hasta construir la recta secante a las dos paralelas deseada. A continuación, mueve el punto Q hasta que los ángulos alternos marcados se superpongan. Comprueba así que los ángulos alternos son iguales.

 

.

 

3. UN PROBLEMA DE ÁNGULOS Y RECTAS PARALELAS

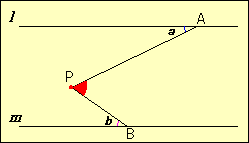
En el dibujo dado, l es paralela a m.

1.- Si el ángulo a = 30 grados y el ángulo b= 45 grados, encuentra el APB.
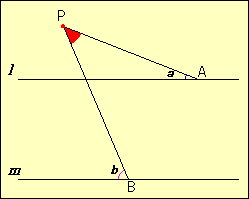
2.- Cuando el punto P está entre las rectas l y m, encuentra la expresión del ángulo APB en función de los ángulos a y b.

 

3.- Si el punto P está por encima de la recta l, encuentra la expresión del ángulo APB en función de los ángulos a y b.

  

 

 

 

Mueve los puntos A y B. Arrastra el punto P y observa las medidas de los distintos ángulos. Puedes utilizar la pista si la necesitas.

 

.

 

 

 

 

 

 

 

 

 

 

 

Fabián Martín Herce

 

Ministerio de Educación, Cultura y Deporte. Año 2007

 

 

 

 

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.