
ALGUNAS FUNCIONES ESPECIALES
2.1 Valor absoluto de una función de segundo grado
Vamos a introducir dos nuevas funciones , la función valor absoluto y la función parte entera como un tipo de funciones que se puede representar a trozos, ambas funciones van a permitir a los alumnos de 4º de E.S.O un acercamiento a las funciones definidas por intervalos y a partir de ellas de forma intuitiva pueden trabajarse contenidos como la continuidad. Es importante que los alumnos empiecen a familiarizarse con estas funciones ya que aquellos que sigan el bachillerato van a encontrarlas de forma habitual dentro del bloque de funciones.
La función valor absoluto asocia a cada número su valor absoluto, es decir su valor prescindiendo del signo, esta función se puede escribir descompuesta en dos tramos:
![]()
En general cualquier función valor absoluto se puede escribir como una función a trozos. Observa la gráfica siguiente y comprueba que el valor absoluto de una función se puede obtener transformando la parte negativa en positiva.
1.- Modifica el valor de la abscisa, x, y observa cómo se obtiene la función valor absoluto al transformar simétricamente el valor negativo de y en su correspondiente valor positivo.
1.- Modifica el parámetro a y comprueba cómo se van obteniendo las distintas funciones valor absoluto.
2.- Expresa cada una de las funciones que obtienes al modificar a como una función a trozos ( debes calcular el punto de corte con el eje de abcisas).
La función valor absoluto de una función de primer grado es continua, decreciente en el primer tramo y creciente en el segundo.
2.1 Valor absoluto de una función cuadrática
Cuando se aplica el valor absoluto a una función cuadrática, dicha función se puede descomponer en tres tramos, los límites de los intervalos que marcan dichos tramos son los puntos de corte de la función cuadrática con el eje de abscisas, por ejemplo:
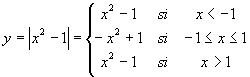
Observa en la siguiente escena que, al igual que en la gráfica del valor absoluto de una función de primer grado, se obtiene también transformando la parte negativa en positiva.
1.- Modifica el valor de la abscisa, x, y observa cómo se obtiene la función valor absoluto al transformar simétricamente el valor negativo de y en su correspondiente valor positivo.
2.- Modifica el parámetro a y comprueba cómo se van obteniendo las distintas funciones valor absoluto.
3.- Expresa cada una de las funciones que obtienes al modificar a como una función a trozos.
4.- Representa y =|x2-4x+3|y exprésala como una función definida en intervalos ( Calcula los puntos de corte de la parábola con el eje x, dichos valores marcarán los extremos de dichos intervalos)
Propuesta de trabajo: dibuja la función seno y a partir de ella dibuja y=|sen x|. Representa ahora la función y=sen|x|, apóyate en una tabla de valores. ¿Coinciden ambas representaciones?¿ Por qué?.
La función signo se define como y = x/|x|, de forma que hace corresponder el valor 1 a los número positivos y -1 a los negativos. Se puede expresar :
![]()
Esta función no está definida en el punto 0, ya que el cociente 0/0 es una indeterminación.
1.Pulsa en el botón del parámetro abscisa y observa qué es lo que ocurre para el valor 0. Define el dominio de dicha función.
La función signo es constante en los dos intervalos y presenta una discontinuidad de salto en el punto (0,0).
La función parte entera y= E(x), hace corresponder a cada número real x, su parte entera. Todo número real está comprendido entre dos números enteros, la parte entera de un número es el menor de los números enteros entre los que está comprendido:
- la parte entera de 1,25 es 1, sin embargo de -1,25 es -2 , ya que -1,25 está comprendido entre -1 y -1 y -2<-1
Es una función constante por intervalos como se puede observar en la siguiente escena:
1.- Modifica la abscisa (x) del control P y observa cómo el punto se desplaza por los distintos tramos.
2. ¿ Es una función continua? ¿ Qué tipo de discontinuidades presenta?. Basándote en tus observaciones define el dominio de esta función.
Muchas situaciones dela vida cotidiana se expresan mediante funciones constantes por intervalos, por ejemplo:
Las tarifas de un aparcamiento indican 0.75 € la hora o fracción hasta un máximo de 12.02 € por día . Haz una gráfica con el importe a abonar por un coche que está aparcado entre 0 y 36 horas. ¿ Cuál es la expresión algebraica de esta función ?
La función parte decimal o función mantisa M(x) = x -E(x) hace corresponder a cada número real x el mismo número menos su parte entera. En la siguiente escena se muestra la representación de dicha función:
1. Modifica el valor de (x) . ¿ Cuál es la parte decimal de 1,70?¿ y de -1,25?. (Ojo con los valores negativos, recuerda que la parte entera de -1,25 es -2)
2.- Observa que al modificar x hay un segmento que se desplaza por los tramos contiguos de la función. Fíjate que los dos puntos marcados tienen la misma imagen y las abscisas se diferencian en una unidad. Es decir si z es un número entero M(x +z*1) =M(x)
Por esta razón decimos que M(x) es periódica y que su periodo es uno.
La función parte decimal es una función definida en intervalos que es siempre positiva o nula, periódica y discontinua en los puntos de abscisa entera.
Autor: J.Carball
| Asturias | ||
| Ministerio de Educación, Cultura y Deporte. Año 2001 | ||
| Castilla y León |