ESPACIO

simetría punto-plano y punto-recta

     1.- Vamos a hallar el simétrico de un punto respecto de un plano en el espacio.

     Comencemos con un caso sencillo, fíjate en la escena: Hemos tomado un punto cualquiera   P(x,y,z)  y calcularemos su simétrico  Q(x',y',z')  respecto al plano  XZ  ( que tiene por ecuación  y=0 ).

     Está claro que solo la coordenada  y'= - y  varía.

   Ejercicio 1.- ¿Cómo sería el simétrico de  P  respecto de los otros planos coordenados?

   Ejercicio 2.- ¿Porqué no trazar la recta que pasa por  P  y es perpendicular al plano dado? ¿Vés que esa recta contiene al simétrico y que el segmento  PQ  tiene como punto medio al punto  M  donde se corta el plano con la perpendicular?

     2.- Vamos a resolver ahora un caso práctico en la escena y con las herramientas de la geometría.

     Ve siguiendo los pasos según se indica debajo, moviendo al tiempo en la escena.

  Paso 1:  Se dan el punto P y el plano  π :   

  Paso 2: Hallamos la recta  r  que pasa por  P  y es perpendicular a  π (recuerda que el vector característico del plano sirve como vector director de la recta) :

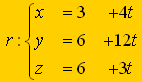   Paso 3:  Nos quedamos con el punto  M  de corte (único) de  r  y  π :

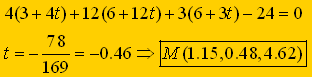    Paso 4:  Nos basamos en que el vector     es doble del vector     . Asi calculamos el simétrico  Q (x,y,z)  buscado.

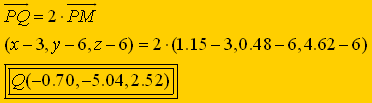      Ejercicio 3.- Halla el simétrico de  P(3,4,-2)  respecto del plano  α : x - y - 2z = 0 .

     3.- Vamos ahora con el simétrico de un punto respecto de una recta.

     Ante todo, no podremos usar el método que ya conocemos de la geometría plana de trazar por el punto la recta perpendicular a la dada, ya que en el espacio hay infinitas rectas ortogonales (que forman un ángulo de 90º con la dada). Pero este hecho nos da la idea:

     Vamos a trazar el plano perpendicular  por el punto a la recta. (Sigue los pasos como en el anterior; ya tienes dibujados punto y recta).

 Paso 1:  Se dan el punto P y la recta  r  :   

  Paso 2: Hallamos el plano  α  que contiene a  P  y es perpendicular a  r (recuerda que el vector vector director de la recta sirve como normal del plano  ) :

   Paso 3:  Nos quedamos con el punto  M  de corte (único) de  r  y  α :

    Paso 4:  Como en el caso anterior, nos basamos en que el vector     es doble del vector     . Asi calculamos el simétrico  Q (x,y,z)  buscado.

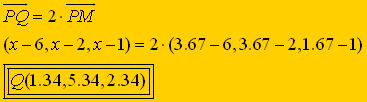Ejercicio 4.- Halla el simétrico de  P(3,4,-2)  respecto de la recta que pasa por los puntos    A(1,-1,-2)  y  B(5,3,2) .

Jesús Antonio SÁNCHEZ MONTERROSO   Ministerio de Educación, Cultura y Deporte. Año 2003

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.