Relaciones entre figuras geométricas en el plano |
|
Construcciones geométricas |
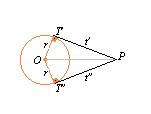
DEBES SABER...
...que para trazar la tangente t´ a una circunferencia en uno de sus puntos T´ basta trazar la perpendicular al radio r que pasa por él.
En este apartado vas a aprender a construir la tangente a una circunferencia desde un punto P exterior.
OBSERVA EL SIGUIENTE NIPPE DESCARTES...
Se trata de dibujar la tangente a la circunferencia de centro O y radio r =3 desde el punto P (10,0)
Hay dos soluciones: la recta PA y la PB simétricas respecto de la recta que une P con O
El punto de contacto A, ha de ser el vértice de un ángulo recto cuyos lados, radio y tangente pasan respectivamente por el centro O y el punto P. Este ángulo abarca, por tanto el diámetro OP de la circunferencia de centro C (punto medio de OP). Lo mismo podemos decir del punto de contacto B. Recordar la propiedad de los ángulos inscritos a una circunferencia que abarcan su diámetro (miden 90º)
Bastará trazar la circunferencia de diámetro OP y unir P con las intersecciones de A y B que produce dicha circunferencia con la circunferencia dada.
| EXPERIMENTA:
El punto P es un control que puedes mover arrastrándolo con el ratón. también puedes cambiar su posición introduciendo sus coordenadas (P.x , P.y) desde la ventana de parámetros. La circunferencia a la que queremos trazar las tangentes, tiene centro O(0,0) y radio r que podemos cambiar introduciendo su valor desde la ventana de parámetros. Observación: Cuando se cambie el valor del radio, no olvidar pulsar limpiar para que se actualice la circunferencia Poner el punto P en (8,-2) e introduce el valor del radio r = 3.5 de la circunferencia de centro O(0,0). Observa que las tangentes a dicha circunferencia desde P se trazan desde P a los puntos de intersección que produce la circunferencia de diámetro OP sobre la circunferencia dada. Comprueba este hecho las veces que quieras cambiando el punto P y el radio de la circunferencia de centro O(0,0) |
PROPIEDAD:
Puesto que las tangentes PA y PB son simétricas respecto de la recta que une P con O se cumplirá que PA = PB
PROBLEMAS:
1.- Dibuja en tu cuaderno una circunferencia de radio 1,5 cm y un punto P que diste del centro de la primera 5 cm.
a) Utilizando la regla y el compás, dibuja las tangentes a la circunferencia trazadas desde P.
b) Mide las tangentes PA y PB y comprueba que tiene el mismo valor.
c) Aplica el Teorema de Pitágoras al triángulo rectángulo OPA para calcular exactamente la longitud de PA. Compara el resultado con el obtenido en el apartado anterior
| Ministerio de Educación, Cultura y Deporte. Año 2000 | Autor: Ángel Cabezudo Bueno | |

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.