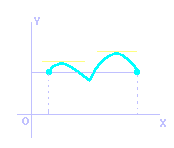Sea una función y=f(x) definida en el dominio D_f

El estudio de la existencia de valores extremos de f(x) nos sirve de modelo para resolver problemas de optimización en diversas situaciones del ámbito económico, científico, técnico,...

El concepto de punto crítico y el de derivada en un punto de la función f(x) nos servirán de herramientas en la localización de valores extremos.

Los puntos singulares son aquellos donde la derivada se anula, f'(x)=0, y la recta tangente a la curva es horizontal.

Estos puntos deben tomarse en cuenta cuando se buscan los extremos absolutos de una función, puesto que en un punto singular puede haber un  máximo o mínimo local. Pero también hay otros en los que debemos fijarnos que sin ser puntos singulares, también pueden ser extremos locales: puntos donde la función no es derivable.

Además, un punto extremo absoluto (máximo o mínimo global) podrá ser encontrado en los extremos a ó b  del intervalo [a,b] donde se define la función.

OBJETIVOS

• Entender el significado de los  teoremas de Weierstrass (de extremos absolutos) y de Rolle y aplicarlos adecuadamente.

• Aprender y utilizar las herramientas de análisis que permiten la localización y cálculo de de los valores extremos (máximos globales o absolutos) de una función en un intervalo cerrado.