FUNCIONES IRRACIONALES
Análisis: Procedimiento para analizar una función
 
1. FUNCIONES IRRACIONALES
Las funciones irracionales son aquellas cuya expresión matemática f(x) presenta un radical:

 

donde g(x) es una función polinómica o una función racional.

Si n es par, el radical está definido para g(x) ³ 0; así que a los efectos de calcular el dominio de f(x) que contenga un radical, habrá que imponer la condición anterior al conjunto de la expresión f(x).

 
 
En el programa siguiente se puede ir siguiendo el proceso constructivo de la función 

 

que es analizada en el ejemplo 1.

Variando el parámetro paso de 1 a 6 irán apareciendo en la escena los distintos elementos  necesarios para poder dibujar la gráfica:

Paso 1: Dominio

Paso 2: Regiones

Paso 3: Asíntotas

Paso 4: Algunos puntos

Paso 5: Monotonía

Paso 6: Trazado de la curva

Observar cómo los pasos que vamos dando se acomodan a las necesidades que vamos teniendo de poder dibujar su gráfica. Conviene situarse en cada nivel de información y ver las posibilidades que puede tener la forma gráfica; en este momento decidimos que herramienta de análisis es la apropiada para aceptar o rechazar posibilidades. Así, en el ejemplo analizado, hemos llegado a un nivel de información en el que se ha hecho necesario conocer algunos puntos de la grafica para comprobar la situación respecto de las asíntotas y todavía ha surgido la necesidad de comprobar si la gráfica cortaba o no a la asíntota oblicua.

Ejercicios:

Analizar y representar las  funciones irracionales,

   

Solución

1

2

3

4

 

El programa siguiente permitirá al estudiante verificar si los resultados de su análisis se corresponden con la información que se visualizan en la escena.

Las ventanas y=f(x), y=a1(x), y=a2(x), y=a3(x), y=a4(x) son funciones editables que el/la estudiante puede reemplazar por las expresiones de Descartes correspondientes de las que tenga interés en ver su representación.

Ejemplo analizado 1:

Analizar y representar la gráfica de la función irracional

 

  1. Dominio:

No está definida para x2-1<0 « x2 < 1 « -1< x < 1. Luego, Df=R-(-1,1).

  1. Cortes con los ejes coordenado:

Corte con OX: y=0.  No es posible.

Corte con OY: x=0. No es posible.

  1. Regiones:

Es fácil comprobar que para x ³ 1, f(x) >0 y para x £ -1, f(x)<0.

  1. Asíntotas:

- Horizontales:

Luego, y=0 es una asíntota horizontal por la derecha. Como,

no hay asíntota horizontal por la izquierda.

- Oblicuas: Probemos si hay asíntota oblicua y=mx+n por la izquierda.

Luego y=2x, es una asíntota oblicua por la izquierda.

  1. Información de la derivada primera:

    Es fácil observar que no se puede anular, por tanto no tiene puntos singulares.

Para x>1, f'(x) <0: f(x) es función decreciente

Para x<-1, f'(x)>0: f(x) es función creciente

  1. Información de la derivada segunda:

Es positiva para todo el dominio: f(x) es función convexa.

  1. Información complementaria:

Con toda la información que ya tenemos puede quedar cierta duda de por donde puede pasar la curva. La siguiente puede darnos la luz necesaria:

- Algunos puntos: x=-1 ® y=-1; x=1 ® y=1

- ¿Atraviesa la asíntota y=2x?: Imposible ya que la ecuación f(x)=2x es incompatible.
       
           
  Ángel Cabezudo Bueno
 
Ministerio de Educación, Cultura y Deporte. Año 2001
 
 

 

Soluciones:

1: Función .

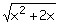a) Dominio: No está definida en el intervalo (-2,0) donde el radicando es negativo

b) Cortes con los ejes: Puntos (0,0) y (-2,0)

c) Regiones: f(x)>0 en (-¥,-2)U(0,+¥)

d) Asíntotas oblicuas: y=x+1, y=-x-1.

Comprobar que no cortan a la curva y que ésta se aproxima por debajo.

e) Información de la derivada primera:

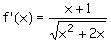
No está definida en [-2,0]. Su signo es el que corresponde a x+1 en el dominio R-[-2,0], luego f'(x) >0, en [0,+¥) y f'(x)<0 en (-¥,-2). Resumiendo:

f(x) es decreciente en (-¥,-2)

f(x) es creciente en   [0,+¥)

No hay singularidades.

Puede observarse que en x=0 y x=-2 la tangente a la curva es vertical (pendiente infinita) tomando límites laterales de f'(x)

f) Datos complementarios:

Es relativamente fácil comprobar que la función f'(x) es decreciente, por lo que f(x) es cóncava. Esto puede observarse en el programa o bien calculando f''(x) y comprobando que es negativa en el dominio.

Volver a los enunciados

2: Función

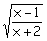
a) Dominio: No está definida en el intervalo [-2,1).

b) Cortes con los ejes: Punto (1,0)

c) Regiones: f(x)>0 en (-¥,-2)U(1,+¥)

d) Asíntotas:

- Horizontal: y=1. No corta la curva y esta se aproxima por arriba para x<-2 y se aproxima por abajo para x>1

- Vertical: x=-2

e) Información de la derivada primera:

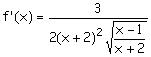
No está definida en [-2,1] y es positiva en todo el dominio. Por tanto f(x) es creciente en su dominio.

No existen singularidades.

Puede comprobarse que la tangente a la curva en x=1 es vertical (pendiente infinita) tomando límite lateral de la función f'(x).

f) Otras informaciones:

No es necesario calcular la derivada segunda para comprobar la forma de la curvatura (cóncava o convexa). Con los datos de que disponemos no puede ser de otra manera que convexa en (-¥,2) y cóncava en (1,+¥). También se puede comprobar sin mucha dificultad que la función f'(x) crece en (-¥,-2) y decrece en (1,+¥) (observar en el programa como varía f'(x)).

Volver a los enunciados

3: Función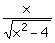

a) Dominio: No está definida en el intervalo [-2,2]

b) Cortes con los ejes: No hay cortes.

c) Simetría: Respecto del origen pues f(-x)=-f(x)

d) Regiones: f(x)>0 para x>2, f(x)<0 para x<-2

e) Asíntotas:

- Horizontales: y=1, y=-1.

No cortan a la curva y ésta se aproxima por arriba para x>2 y por abajo para x<-2.

- Verticales: x=2, x=-2

f) Información de la derivada primera:

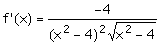
No está definida en el intervalo [-2,2].

f'(x) <0 en el dominio, por tanto f(x) es decreciente.

f) Otras informaciones:

No es necesario calcular la derivada segunda para comprobar la forma de la curvatura (cóncava o convexa). Con los datos de que disponemos no puede ser de otra manera que convexa en (2,+¥) y cóncava en (-¥,-2).

Volver a los enunciados

4: Función

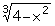
a) Dominio: (-¥,+¥)

b) Cortes con los ejes: (0, raiz3(4)) , (2,0) y (-2,0)

c) Simetría: Respecto del eje OY pues f(x)=f(-x)

d) Regiones: f(x)>0 en el intervalo (-2,2) y f(x)<0 en (-¥,-2)U(2,+¥)

e) Ramas parabólicas:  Comprobar analíticamente que el tipo de ramas parabólicas que presenta son tales que tienen pendiente nula en el infinito, m=lím f(x)/x=0 

No hay asíntotas. 

f) Información de la derivada primera:

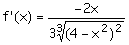
No está definida en x= 2 y x=-2. En estos puntos la tangente es vertical (pendiente infinita)

f'(x) >0 en (-¥,0): f(x) creciente

f'(x)=0 en x=0: Máximo relativo

f'(x)<0 en x>0: f(x) decreciente

g) Otras informaciones: La expresión de la derivada segunda de f(x) se complica lo suficiente  para que la desechemos como herramienta que nos permita averiguar la concavidad y convexidad. Si pensamos que la curva es simétrica respecto de OY y solo es necesario observar para x>0,  caeremos en la cuenta de lo siguiente:

- El máximo en x=0 y la tangente infinita (-¥) en x=2 no advierte que la función f'(x) decrece en el intervalo (0,2), es decir que en (0,2) hay concavidad pues f''(x) tiene que ser negativa.

- Tipo de rama parabólica que presenta  nos informa que tiene pendiente nula en el infinito por lo que la función f'(x) en el intervalo (2,+¥) tiene que crecer y f''(x)>0; es decir que en (2,+¥) hay convexidad.

- De los dos apartados anteriores deducimos que en x=2 y en x=-2 cambia la forma de la curvatura; dichos puntos son de inflexión y con pendiente vertical.

Observación: es muy instructivo representar en el programa la función f'(x). Reemplazar la entrada editable f(x) por la correspondiente a f'(x)=-2*x/(3*((4-x^2)^2)^(1/3)) y se observará el crecimiento y decrecimiento de la misma a los efectos de comprobar la concavidad y convexidad de f(x).

Volver a los enunciados

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.