Vectores

	VECTORES
	Geometría

1. VECTORES EQUIPOLENTES

Cuando movemos una figura en el plano la desplazamos una determinada cantidad en una dirección y un sentido. Un vector V está formado por todas las flechas que indican la magnitud, orientación y sentido de ese desplazamiento. Si tomamos una de esas flechas cuyo origen coincida con el origen de coordenadas, a las coordenadas (x,y) del extremo de ese vector se les llama coordenadas del vector.

Todas las flechas paralelas a ésta con el mismo sentido y tamaño se les llama equipolentes a la primera. La escena Descartes siguiente nos permite visualizar todas las flechas asociadas a un vector de coordenadas (Vx,Vy) y en la que varían las coordenadas del origen y extremo de las respectivas flechas pero no así las que tiene como vector.

1.- Arrastra con el ratón el origen del vector y muévelo por toda la escena.

2.- Representa en tu cuaderno el vector (-3,-2) y dibuja cuatro representantes con origen en cada uno de los cuadrantes.

3.- Repite la operación con los vectores (4,-3), (-5,3) y (5,2).

Pulsa el botón Inicio y mueve el origen del vector a la posición (-3,2). Observa cómo las coordenadas del vector se obtiene de restar a las coordenadas del origen las del extremo, es decir: Vx=0-(-3)=3; Vy=1-(-2)=3. Cambia el origen a otra posición y comprueba cómo se cumple siempre esa relación.

4.- Representa en tu cuaderno un vector cuyo origen sea (1,0) y el extremo (-4,1) y calcula sus coordenadas. Comprueba con Descartes el resultado introduciendo primero las coordenadas y luego moviendo el vector hasta ver si coincide con los dos puntos dados.

2. Coordenadas de un vector
Para facilitar el cálculo de las coordenadas de un vector la escena Descartes de la izquierda dibuja un vector al azar cada vez que se pulsa el botón Inicio.

5.- Dibuja el vector que aparece en la escena izquierda en tu cuaderno y halla sus coordenadas. Comprueba después, en la escena de la derecha, que las coordenadas que has calculado son las correctas. Para ello mueve el origen del vector al punto donde se encuentra e introduce las coordenadas hasta encontrar un vector equivalente. Cada vez que pulsas el botón Inicio vuelve a aparecer un nuevo vector. Repite la operación al menos 10 veces.

3. Suma de vectores libres

Dados dos vectores U y V se define la suma como el vector S cuyas coordenadas son la suma de las coordenadas de cada uno de ellos.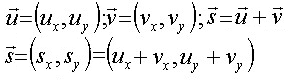

Para introducir vectores diferentes puedes también arrastrar los puntos rojos con el ratón en lugar de introducir sus coordenadas en la línea inferior

6.- Calcula la suma de los vectores U=(5,2) y V=(1,3). Halla las coordenadas del vector suma y represéntalo en tu cuaderno, compara con el resultado en la escena Descartes.

7.- Repite la operación con los vectores U=(-2,3) y V=(2,-3).

8.- Dos vectores son opuestos cuando al sumarlos dan el vector (0,0) ¿Dado el vector U=(2,-3) cómo serán las coordenadas del vector opuesto?

9.- ¿Qué relación hay entre las coordenadas de un vector y su opuesto?

	Miguel García Reyes

	Ministerio de Educación, Cultura y Deporte. Año 2001

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.