 Lugares geométricos
Lugares geométricos Lugares geométricos
Lugares geométricos
3. La circunferencia:
a) Circunferencia como lugar geométrico
b) Ecuación de la circunferencia
c) Recta tangente a una circunferencia en un punto
d) Recta normal a una circunferencia en un punto
e) Circunferencia conocido el diámetro
a) Circunferencia como lugar geométrico:
Sea un punto C (a,b) y un nš positivo r, la circunferencia de centro C y radio r es el lugar geométrico de los puntos P (x,y) cuya distancia al punto C es r.
Condición:
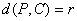
|
|
b) Ecuación de la circunferencia:
Sea un punto C (a,b) y un nš positivo r, la ecuación de la circunferencia de centro C y radio r es:
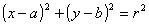
Esta ecuación se obtiene elevando al cuadrado los dos miembros de la expresión anterior.
B1.- Halla la circunferencia con un centro y un radio dado: (Para cada caso coloca el punto C en la posición que se indica, introduce el valor del radio y obtendrás la ecuación de la circunferencia en la parte superior izquierda)
|
Centro y radio |
Ecuación de la circunferencia |
| a) C(3,-1) y r=2 | |
| b) C(3,4) y r=3 | |
| c) C(-2,2) y r=4 | |
| d) C(4,1) y r=3 |
c) Recta tangente a una circunferencia en un punto:
Sea la circunferencia de centro C (a, b), la recta tangente en el punto P (x0,y0) la podemos hallar con la expresión:
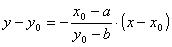
Otra forma (como muestra la actividad) es:
Paso 1:
Calculo el vector CP
Paso 2:
El vector CP es el vector normal de la recta tangente a la circunferencia en el punto P.
Paso 3:
Hago pasar la recta por el punto P.
Paso 4:
Aparece la recta tangente a la circunferencia por el punto P.
C1.- Halla la recta tangente a una circunferencia dada que pase por un punto dado: (Para cada caso introduce el valor del centro y del radio de la circunferencia así como del punto de tangencia y realiza los 4 pasos de la actividad.)
|
Centro y radio; punto |
Recta tangente |
| a) C(2,1) , r=2 ; P(2.5 , 2.94) | |
| b) C(3,2) , r=3 ; P(2 , 0.83) | |
| c) C(0,0) , r=3 ; P(1 , 2.83) | |
| d) C(-1,1) , r=4 ; P(2.46 , 3) |
d) Recta normal a una circunferencia en un punto:
Sea la circunferencia de centro C (a, b), la recta normal en el punto P (x0,y0) la podemos hallar con la expresión:
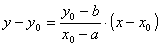
Otra forma (como muestra la actividad) es:
Paso 1:
Calculo el vector CP
Paso 2:
El vector CP es el vector director de la recta normal a la circunferencia en el punto P.
Paso 3:
Hago pasar la recta por el punto P.
Paso 4:
Aparece la recta normal a la circunferencia por el punto P.
D1.- Halla la recta normal a una circunferencia dada que pase por un punto dado: (Para cada caso introduce el valor del centro y del radio de la circunferencia así como del punto y realiza los 4 pasos de la actividad.)
|
Centro y radio; punto |
Recta normal |
| a) C(1,-1) , r=3 ; P(4 , -1) | |
| b) C(-2,2) , r=3 ; P(-1.25 , -0.90) | |
| c) C(0,0) , r=3 ; P(1 , 2.83) | |
| d) C(-5,-3) , r=4 ; P(-1.85 , -0.53) |
e) Circunferencia conocido el diámetro:
Sea el punto P y el punto Q que forman el diámetro de una circunferencia:
Paso 1:
Hallar el centro de la circunferencia como punto medio de los puntos que definen el diámetro.
Paso 2:
Hallar el radio como la mitad de la distancia entre los puntos que definen el diámetro.
Paso 3:
Con el centro y el radio hallo la ecuación de la circunferencia.
Paso 4:
Dibujar la circunferencia.
E1.- Halla la circunferencia cuyo diámetro es el segmento formado por las siguientes parejas de puntos: (Para cada caso sitúa los puntos en el lugar indicado y realiza los 4 pasos de la actividad.)
|
Diámetro |
Circunferencia |
| a) P(3 , 4) , Q(-3 , -4) | |
| b) P(4 , 0) , Q(0 , 6) | |
| c) P(0 , 0) , Q(4 , 4) | |
| d) P(-4 , 0) , Q(4 , 0) |
|

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.