
 |
Interpretación de gráficas. |
| Análisis | |
| Dos ejemplos sencillos. | |||||||||||||||||||
|
1. El precio de un bolígrafo en la
papelería cercana es de 0,30 €.
Calcula y escribe en la tabla
siguiente el precio de los bolígrafos que se indican.
bolígrafos precio | |||||||||||||||||||
|
Esta tabla se llama tabla de
valores.
En la escena siguiente hemos dibujado unos ejes
coordenados. En el eje horizontal representamos el número de
bolígrafos que compramos. En el eje vertical representamos el
precio de la compra. Para cada valor que le asignes al número de
bolígrafos se marca en su vertical el precio de esos bolígrafos
con un punto rojo.
En la parte inferior de la
escena asígnale a la variable bolígrafos los valores de la
tabla anterior y observa su precio, es decir, la altura donde se
coloca el punto rojo.
| |||||||||||||||||||
|
- ¿Qué mide un cuadradito cualquiera del eje horizontal? | |||||||||||||||||||
|
- ¿Qué mide un cuadradito cualquiera del eje vertical? | |||||||||||||||||||
|
- Fijándote en la gráfica, ¿cuánto cuestan 16 bolígrafos? ¿Cuántos bolígrafos te dan por 3,60 €? | |||||||||||||||||||
|
- ¿Tiene sentido unir los puntos rojos de la gráfica? ¿Por qué? | |||||||||||||||||||
|
2. El siguiente ejemplo es muy
similar al anterior. Queremos comprar patatas a 0,30 € el
kilo. Podemos construir una tabla y una gráfica idénticas a las
anteriores salvo que en el eje horizontal representamos los kilos
de patatas.
Pero hay una importante diferencia
entre ambos ejemplos: no podemos comprar fracciones de
bolígrafos (1,5 o 2,7 bolígrafos) y en cambio sí podemos
comprar fracciones de kilos de patatas (1,5 o 2,7 kilos de
patatas).
Calcula y anota los precios de las siguientes
cantidades de patatas. Asígnale esos valores a la variable kilos
de la escena siguiente.
kilos de patatas precio | |||||||||||||||||||
|
¿Tiene sentido ahora unir los
puntos rojos de la gráfica?
Compuébalo en la escena
asignándole a la variable kilos el valor 0 y a continuación,
mantén pulsado el botón del ratón sobre la fecha superior de
los kilos de patatas.
| |||||||||||||||||||
|
En el primer caso, la gráfica está formada por puntos aislados. En el segundo caso, la gráfica es una curva (en este caso, una recta) continua. | |||||||||||||||||||
|
La gráfica de las
funciones lineales
La relación entre las dos
variables de las dos funciones anteriores se presenta muy a
menudo en la vida cotidiana. Como sabes, esta relación se llama
proporcionalidad directa: el cociente entre las dos variables, el
precio del producto y su cantidad, se mantiene constante. Las
funciones de proporcionalidad se llaman también funciones
lineales. Sus gráficas siempre son rectas que pasan por el
origen de coordenadas.
| |||||||||||||||||||
| Más ejemplos. | |
|
3. Este verano mi familia y yo nos iremos de vacaciones a la costa en nuestro coche. Debemos recorrer un total de 800 km. En la escena siguiente representamos la gráfica de nuestro recorrido. En el eje horizontal marcamos el tiempo de viaje, en el eje vertical, el espacio recorrido. | |
|
Asígnale a la variable horas los valores 1, 2, 4 y 8. Anota en tu cuaderno el espacio recorrido en cada caso. Observa que el cociente entre el espacio y el tiempo es siempre constante = 80, es decir, las dos variables son proporcionales, la función es lineal. En nuestro ejemplo, la razón de la proporción mide la velocidad del coche. | |
|
Modifica el valor de la velocidad a 100 km/h. Observa cómo se modifica la gráfica de la función. Asigna de nuevo a la variable horas los valores 1, 2, 4 y 8 y anota el espacio recorrido con esta nueva velocidad. Igual que antes, el cociente entre el espacio recorrido y el tiempo que ha tardado en recorrerlo es constante, pero ahora su valor es 100. | |
|
Asígnale a la variable velocidad distintos valores y observa la variación de la gráfica y de los valores del espacio recorrido. | |
|
La razón de la proporción en las funciones lineales mide la pendiente de la recta que representa la función. | |
| Características de las gráficas. | |||||||||||||||||||||||||||||
|
4. La siguiente gráfica muestra
las temperaturas a lo largo de un día de invierno en un pueblo
de Valladolid. En el eje horizontal hemos representado las horas
del día y en el eje vertical, las temperaturas.
Cuando éstas aumentan decimos que
la función es creciente. Cuando disminuyen, diremos que es
decreciente.
En aquellos puntos de la gráfica
de una función donde pasa de ser decreciente a ser creciente
decimos que alcanza un mínimo. En los puntos que pasa de ser
creciente a ser decreciente alcanza un máximo.
| |||||||||||||||||||||||||||||
|
¿Qué temperatura hizo a las 0 horas? ¿Y a las 10 horas? | |||||||||||||||||||||||||||||
|
¿A qué hora había 0º? | |||||||||||||||||||||||||||||
|
¿A qué hora se alcanzó la temperatura máxima del día?¿Cuál fue la temperatura máxima? | |||||||||||||||||||||||||||||
|
¿A qué hora se alcanzo la temperatura mínima del día? ¿Cuál fue la temperatura mínima? | |||||||||||||||||||||||||||||
|
¿En que periodo del día subió la temperatura? ¿En qué periodo bajó? ¿En qué periodos se mantuvo constante? | |||||||||||||||||||||||||||||
|
¿En qué período del día hubo una temperatura por debajo de 0º? | |||||||||||||||||||||||||||||
|
Construye una tabla con las
temperaturas que se registraron a lo largo del día.
| |||||||||||||||||||||||||||||
|
5. En la siguiente escena se representa la gráfica de una función creciente en el intervalo [0,8], decreciente en el intervalo [8,16] y creciente de nuevo en el intervalo [16,24]. La función alcanza un máximo en el punto B y un mínimo en el punto C. Arrastra los puntos A, B, C y D para representar gráficas con las siguientes características. EN cada caso, escribe en tu cuaderno en qué intervalos la función es creciente y en cuáles es decreciente: | |||||||||||||||||||||||||||||
|
Pasa por los puntos (0,3) y (24,0), alcanza un máximo en el punto (8,6), un mínimo en el punto (16,-5). | |||||||||||||||||||||||||||||
|
Pasa por los puntos (0,0) y (24,0), alcanza un mínimo en el punto (8,-7), un máximo en el punto (16,3). | |||||||||||||||||||||||||||||
|
Pasa por los puntos (0,5) y se mantiene constante = 5 en todo el intervalo. | |||||||||||||||||||||||||||||
|
Pasa por el (0,0) y por el (8,2) y es una función lineal. | |||||||||||||||||||||||||||||
|
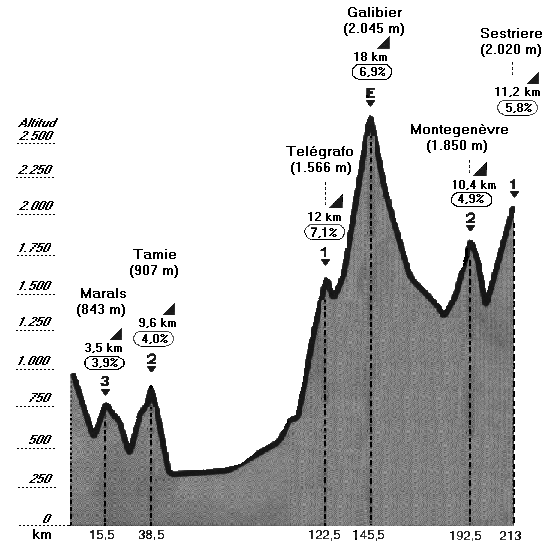
6. La siguiente gráfica representa el perfil de la 9ª etapa del Tour de Francia del año 1999 Le Grand Bornard-Sestriere. Se subieron seis puertos de montaña de los Alpes. | |||||||||||||||||||||||||||||
|
¿Cuántos kilómetros tiene la etapa? | ||||||||||||||||||||||||||||
|
¿En qué puntos kilométricos de la etapa presenta la gráfica un máximo y qué altitud alcanza en cada uno? | |||||||||||||||||||||||||||||
|
¿En qué puerto se alcanza la mayor altitud? ¿Qué puerto de montaña tiene mayor longitud? ¿Y en cuál hay mayor pendiente? | |||||||||||||||||||||||||||||
|
Describe el recorrido de la etapa a la vista de los datos que aparecen en la gráfica. | |||||||||||||||||||||||||||||
| Fernando Arias Fernández-Pérez | ||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2001 | ||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.