
PROPIEDADES DE LA INTEGRAL DEFINIDA
Pulsa en los recuadros azules para ver el significado geométrico
de las propiedades
-
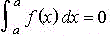
-
Si
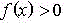 en todo
el intervalo, entonces
en todo
el intervalo, entonces 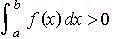 .
.
Análogamente si 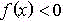 .
.
-
Si
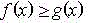 para cualquier
valor
para cualquier
valor 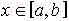 , entonces
, entonces 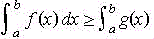
-
Si f es continua en [a,b],
[a,c] y [c,b],
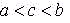 ,
entonces
,
entonces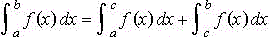
-
Si f es continua en [a,b],
entonces
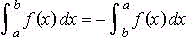
-
Si f es continua en [a,b]
y k es una constante, entonces
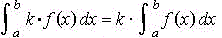
-
Si f y g son continuas en [a,b],
entonces
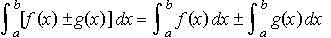
Autor: José Mª Domínguez
Torres
