

LA INTEGRAL DEFINIDA
Integral de una función
Sea y = f(x) una función, con valores no negativos en un intervalo [a, b] continua.
1.- Dividimos el intervalo [a, b] en n partes iguales, vamos a aproximar el valor del área comprendida entre la curva y eje OX, para ello construimos los rectángulos de base la partición definida en el intervalo [a, b] y de altura, en el primer paso el valor mínimo de la función y = f(x), y en el segundo paso el valor máximo. Con todo ello conseguimos una aproximación por defecto del área y otra por exceso.
Con el botón sumas veremos la aproximación por exceso y por defecto, variando el valor de 1 a 0.
Inicio y final nos dan los valores del intervalo [a, b].
Divisiones nos da el número de divisiones del intervalo [a, b]. Cuantas mas tengamos mas cerca estará del valor del área.
A este límite lo llamaremos integral de la función y = f(x) y lo denotaremos por:
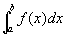
Área comprendida entre una curva y el eje OX.
Observa el área comprendida entre la curva y el eje OX.
Varia los valores de a y b. El área comprendida entre las rectas x =a, x = b, el eje OX y la curva es
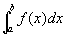
1.- Halla el área comprendida entre la curva y = 3x + 2 entre los valores de x = 1 y x= 4. Comprueba que coincide con el área del trapecio formado.
Área comprendida entre dos curvas
Dadas dos curvas para hallar el área comprendida entre ellas solo tendremos que restar el área comprendida entre la superior y el eje de las x y la inferior y el eje de las x. es decir hallar
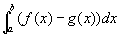
2.- Define y dibuja dos parábolas, una con el coeficiente de grado 2 positivo y otra con el coeficiente de grado 2 negativo y halla el área encerrada entre ellas.
3.- Halla el área comprendida entre la parábola
![]()
|
|||||||||||||||