
 |
APLICACIONES DE LA INTEGRAL DEFINIDA. CÁLCULO DE ÁREAS |
| 2º Bachillerato Ciencias Sociales | |
| 2.- EL SIGNO DE LA INTEGRAL | |||
Para hallar el signo de la integral 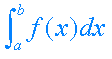 , realiza los ejercicios
que se proponen en la siguiente escena. , realiza los ejercicios
que se proponen en la siguiente escena. Se pueden deducir las siguientes propiedades:
|
|||
|
|||
| Anota en tu cuaderno: 1) Aplicando la Regla de Barrow calcula la integral de f(x) = x2-1 entre a=1, b=2 2) ¿Qué signo tiene la integral? 3) Calcula, modificando los valores de a,b la integral de f(x) = x2-1 entre a=-1 , b=1 4) ¿Qué signo tiene ahora la integral? 5) Calcula, modificando los valores de a,b la integral de f(x) = x2-1 entre a=-1 , b=2. 6) ¿Cuánto vale la integral ?. 7) Intenta
encontrar una relación entre el signo de la función f(x) y el signo de la integral.
|
|||
| Mª Dolores Chávez Gordito | |
 |
|
| Ministerio de Educación, Cultura y Deporte. Año 2003 | |