
INTEGRACIÓN
INTEGRAL DEFINIDA
Área del plano definida por la gráfica de una función, el eje OX y las rectas x=a y x=b
Dada una función, vamos a representar la región del plano comprendida entre su gráfica, el eje OX y las rectas x=a y x=b, donde a y b son dos valores previamente establecidos.
Por ejemplo, si
y los puntos establecidos son
a = 0
b = 3
la región del plano sería :
Propuesta de trabajo:
Observa detenidamente la región coloreada en turquesa y que se encuentra comprendida entre
el eje OX
la recta x = a
la recta x = b
la gráfica de la función y=f(x)
Para calcular el área de esa región podríamos dividirla en pequeñas áreas semejantes a las que aparecen en la siguiente figura y después sumarlas.
Cada una de esas áreas pueden volver a dividirse en otras más pequeñas y así sucesivamente hasta obtener una infinidad de barras de altura el valor de la función en cada punto y de ancho un valor muy pequeño al que llamaremos dx. Entonces, el área de toda la región será:
Suma desde a hasta b de f(x).dx
que para abreviar representamos de la forma:
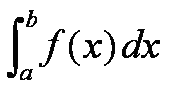
y que llamamos integral definida desde a hasta b de la función f(x).
Propuesta de trabajo:
Observa la gráfica siguiente e intenta averiguar aproximadamente y sirviéndote de los cuadritos de los ejes (cada uno vale 1 unidad cuadrada) el valor de
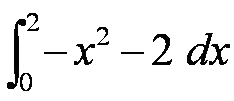
Pero ┐Qué signo le pondrías? , ┐negativo o positivo?.
Algo más difícil: ┐Cuál será el valor de la integral en el siguiente gráfico?
Anota todas las respuestas en tu cuaderno.
Para saber las respuestas pincha aquí
Autor: Nombre y apellidos