
 |
THE DEFINITE INTEGRAL |
| 1. THE DEFINITION OF THE INTEGRAL OF A FUNCTION |
|
If we make n (the number of partitions) tend towards infinity, which is the same as making the rectangle bases tend towards zero, we could find the limit of both the upper and lower Reimann sums. If both limits exist and they are equal then we can say that the function f can be integrated and the definite integral of f between a and b can be defined as the result of this limit, therefore: At each end of the interval a and b are called the upper and lower limits of integration respectively. |
| 2. THE SIGN OF THE DEFINITE INTEGRAL | |||
|
According to the definition of the definite integral, there is an intrinsic relation between this concept and the area of the trapezium-like shape. But is it the same? |
|||
1.- Look carefully at the following window. All the functions which appear are constant but are not necessarily positive. Compare the value given for the bounded area with the definite integral on this interval. Are the two concepts exactly the same?
2.- Analyse the definition of the definite integral and try to explain it. 3.- Determine the relation between the bounded area and the definite integral for negative functions. 4.- Is it possible to have a bounded area whose area is not zero but a definite integral with a value of 0? Give some examples. |
|||
| 5.- State the relation between the sign of the function and the sign of the defined integral of the function. | |||
| 3. BASIC PROPERTIES OF THE DEFINITE INTEGRAL | |||
If
c is a point within the interval [a,b],
then 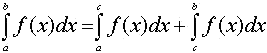 |
|||
6.- Look carefully at the relation between the pink and yellow areas. Find a relationship between the integral of a function between a and b and the integrals of the same function between [a,c] and [c,b]. 7.- Can we generalise the result for functions which are not necessarily positive?
|
|||
|
The definite integral of a function f when a=b is equal to zero. |
|
8.- Change the value of b and look carefully at the results. 9.- Proof the result analytically. 10.- Is it true to say that b1<b2 so the integral between a and b1 is less than the integral between a and b2? When is this true? 11.- When we have two different functions, f1 and f2 , and f1<f2, is the integral between a and b of f1 less than the integral between a and b of f2? 12.- Can we generalise the result for function which are not necessarily positive? 13.- Explain the result below analytically using properties 1 and 2. |
|
| 14.- Could this result have been deduced from the results of activity 2? | |
The
definite integral is linear.
|
|||||
15.- This window illustrates two functions f and g and the sum of these functions h. Check that the relation h(x)=f(x)+g(x) is true for any value of x.
16.- Look carefully at the relation between the rectangles used in the Reimann's sums for f, g and h.
|
|||||
| 17.- State the relation
between the integrals of f and g and their sum f+g. Is this relation the
same when finding the difference? Clue: Use
the properties of the limits.
18.-What relation is there between the integral of a function and the integral of double the same function? 19.- State the property which relates the integral of a function multiplied by a real number and the integral of that function. |
|||||
| 4. MEAN VALUE THEOREM | |
|
Given a continuous function f defined on
[a,b], value c exists such that |
|
20.- Look carefully at the rectangles which have been chosen in each partition and the result of the grey and orange areas. What happens? Why? 21.- Find the areas of the rectangles which are being used to evaluate the integral. Why is there a value of x on the base of each rectangle such that the image of the function at this point is a height which when multiplied by the base gives the exact area of the orange area we want to find? Which well-known theorem is being referred to here? 22.- Find the formulae of the rectangles which through under and over estimation are used to evaluate the orange area when n=1. |
|
23.-
Compare the formulae
obtained in the exercise above with the orange area. Find the
following inequality  where
m and M are the minimum and maximum of f on [a,b] respectively. where
m and M are the minimum and maximum of f on [a,b] respectively.
24.- Use the intermediate value theorem for the function f and demonstrate the mean value theorem. |
|
| 5. THE ABSOLUTE VALUE OF AN INTEGRAL AND THE INTEGRAL OF AN ABSOLUTE VALUE | ||
24.- Look carefully at the graphs of function f and the absolute value of this function |f|. The area bounded by the curve and the X-axis is the same in both cases. However, are the definite integrals of f and |f| the same? 25.- Determine when both integrals are the same. 26.- What relation of order is there between the absolute value of the integral of a function and the integral of the absolute value of the same function?
|
||
Given a function f it is true to say that
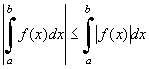
|
||
| Enrique Martínez Arcos | |
 |
|
| Spanish Ministry of Education. Year 2001 | |

Except where otherwise noted, this work is licensed under a Creative Common License