 |
UNIDAD DIDÁCTICA: Fracciones y Porcentajes
|
| 2º de ESO | |
 |
UNIDAD DIDÁCTICA: Fracciones y Porcentajes
|
| 2º de ESO | |
|
AUMENTO Y DISMINUCIÓN DEL PORCENTAJE |
|
AUMENTAR O DISMINUIR UN NÚMERO EN UN PORCENTAJE
Cuando una cantidad (que es el 100%) aumenta o disminuye en un porcentaje, se convierte en otra cantidad.
En un problema de aumentar y disminuir un porcentaje puede pedirnos tres cosas:
|
CASO 1: ¿EN QUÉ SE CONVIERTE...?
Problema: En un restaurante, al menú de 9¤, hay que añadirle el 7% de I.V.A. ¿cuánto cuesta?
Solución: El precio base es 9¤. El 7% es de los 9¤, así que el 100% es 9.
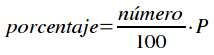 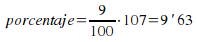 |
||||||
|
CASO 2: ¿QUÉ TANTO POR CIENTO...?
Problema: En abril del año pasado, cayeron en una ciudad 55mm de lluvia por metro cuadrado. En mayo de este año han sido 59mm. ¿Cómo ha variado en porcentaje?
Solución: El porcentaje hay que darlo respecto al valor antiguo, así que este (55) será el 100%. Lo que nos pregunta es qué porcentaje de ese valor es el nuevo valor (59). Esto lo hacemos con una regla de tres:
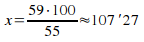 |
CASO 3: ¿CUÁNTO ERA ANTES?
Problema:Un ordenador cuesta 560 euros, que es un 20% menos que hace 3 meses. ¿Cuánto costaba entonces?
Solución: Como siempre, el porcentaje hay que darlo respecto al valor antiguo, así que este será el 100%. Pero eso es el que queremos hallar.
|
| Carlos López Yrigaray | ||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2009 | ||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.