Determinantes de orden 3
Definición del determinante de orden 3
Orientación en IR³
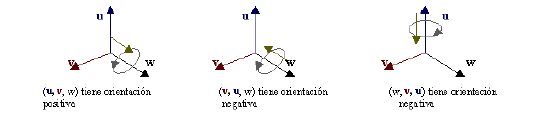
Una base (u, v, w) de R3 (tres vectores que determinan un paralelepípedo) tiene una orientación positiva o negativa, buena o mala orientación se suele decir también. Al estar en dimensión 3, podemos ver la base (u, v) del plano <u, v> con orientación positiva, (ahora se puede ver la otra cara del plano), pues bien, si viendo el plano <u, v> con esta orientación resulta que w indica altura, diremos que la base (u, v, w) está bien orientada; si por el contrario w indica bajura, diremos que dicha base está mal orientada.
Ejemplos:

Así pues una base bien orientada se puede ver como (Este, Norte o NE o NO, Altura).
Al igual que en dimensión 2, el concepto de orientación también se puede definir con el sentido del ángulo entre vectores:
Se dice que una base (u, v, w) tiene orientación positiva si al girar un tornillo, con la dirección de w, en el sentido rotatorio de u a v, este avanza en el sentido de w; cuando el tornillo avance en sentido contrario a w, se dirá que la orientación de la base es negativa.
Ejemplos:

Obsérvese que al trasponer dos vectores de una base, la orientación cambia de signo:

Determinante de orden 3 = Volumen orientado

Diremos que el volumen del paralelepípedo determinado por 3 vectores (u, v, w) es positivo o negativo según sea la orientación de la base (u, v, w): 

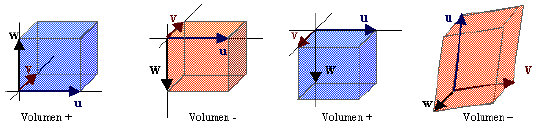
Este concepto coincide con la definición de volumen = área de la base · altura, cuando estas se toman orientadas.

Definición: 

El determinante de tres vectores en IR³ (u, v, w) es el volumen orientado del paralelepípedo que determinan, designaremos este volumen por det(u, v, w). Si uno de los vectores u, v, w, es combinación lineal de los otros, es decir, si
los tres vectores están en el mismo plano, det(u, v, w) = 0, pues la altura de este paralelepípedo es 0.

Propiedades de los determinantes
1 Si a una fila se le suma una combinación lineal de las otras, el determinante no varía
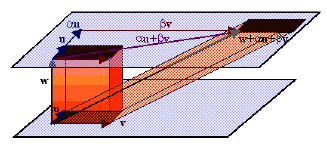
En la figura vemos que al sumarle al 3º vector-fila una combinación lineal del 1º y del 2º, se obtiene otro paralelepípedo con la misma base y la misma altura, luego el determinante no varía.

2 El determinante es una forma hemisimétrica
Al permutar dos vectores-fila de una matriz su determinante cambia de signo pero no de valor absoluto. Esta propiedad ya se ha visto al estudiar la orientación en este capítulo:

det(u, v, w)= -det(v, u, w)

3 El determinante es una forma multilineal
3.a) det(u, v, w)=·det(u, v, w) para cualquier número real

3.b) det(u, v, w1 + w2)=det(u, v, w1)+det(u, v, w2)

4 El determinante de la matriz identidad es 1
Pues el volumen que determina dicha matriz es el de un cubo de lado unidad

Cálculo del determinante de una matriz de orden 3
Sean i=(1, 0, 0), j=(0, 1, 0) y k=(0, 0, 1)

Eliminamos los determinantes que no definen volumen por ser de vectores coplanarios y aplicando ahora las propiedades 2 y 4 obtenemos que:

Geométricamente el paralelepípedo que determinan los vectores fila se ha descompuesto en seis paralelepípedos paralelos a los ejes de coordenadas

Determinante del producto

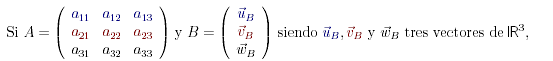
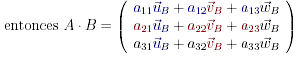
y sus filas son las de A al tomar como base los vectores fila de B. Así pues, el detA·B es el de A multiplicado por el volumen del paralelepípedo que determinan (u_B, v_B, w_B) con lo que se concluye que el determinante del producto es el producto de los determinantes.

El determinante de una matriz es igual al de su traspuesta

Esta propiedad admite en este orden la misma demostraciónn aritmética que se describió para los determinantes de orden 2. Por tanto, las propiedades descritas para las filas de un determinante son tambi´en ciertas para las columnas.

Desarrollo de un determinante por los elementos de una fila

Llamaremos menor de fila i y columna j, mij, al determinante que resulta al eliminar en la matriz A la fila i y la columna j. El adjunto Aij es igual a (-1)i+j·mij

Observación

Pues volumen=área·altura y en este caso el primer vector fila (altura) es perpendicular a los otros 2 (base)

Desarrollo del detA por los elementos de la primera fila

Desarrollo del detA por los elementos de la fila i

Basta aplicar (i-1) trasposiciones a las filas de A para tener:

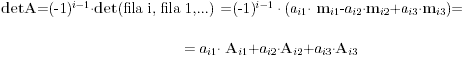
Definición de determinante de orden n

Ampliamos ahora el determinante a matrices de orden n generalizando la fórmula obtenida para n igual a 2 y a 3:

Sea A = (aij) una matriz cuadrada de orden n, se define el determinante de A como:

Esta fórmula extiende a orden n el concepto de longitudes, áreas y volúmenes orientados y verifica las propiedades que se vieron para el orden 2 y 3.

Consolación Ruiz Gil