|
|
||
| Geometría | ||
|
|
||
| ÍNDICE | ||
|
Demostración Teorema de Pitágoras |
||
|
||
|
||
|
Haz
coincidir al ángulo A del
triángulo rosa con el ángulo A del
amarillo y fijate como la altura del triangulo amarillo divide al rosa,
dejando un pequeño triángulo rosa por encima de la altura y
que
este es igual al pequeño triángulo amarillo que queda por debajo de la
altura.
Repitelo
con el ángulo B y el triángulo
azul.
|
||
|
||
| Explica por qué el área del triángulo amarillo es la suma del área del triángulo rosa y del triángulo azul | ||
| Explica en tu cuaderno por qué los tres triángulos son semejantes | ||
|
Copia en tu cuaderno la demostración del Teorema de Pitágoras |
||
|
||
En un triángulo rectángulo al trazar la altura de la hipotenusa se forman dos triángulos rectángulos semejantes entre sí y semejantes con el triángulo de partida
Los tres triángulos son semejantes
Tienen sus lados homólogos proporcionales:
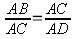
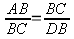
Producto de los medios igual al producto de los extremos
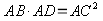
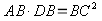
Sumando miembro a miembro
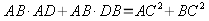
Sacando factor común
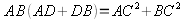

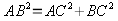
El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos
Teorema de Pitágoras

