ECUACIONES PARAMÉTRICAS  EN EL PLANO
Geometría
 
1. ECUACIONES PARAMÉTRICAS DE LA CIRCUNFERENCIA
Cuando estudiamos la circunferencia llegamos a la conclusión de que x2+y2=r2 es la ecuación de una circunferencia con centro en el origen y radio r. Otra forma de considerar la relación que cumplen las coordenadas de los puntos de una circunferencia es la siguiente: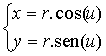
 
La demostración es sencilla: se elevan al cuadrado estas ecuaciones y se suman, en la ecuación resultante se tiene en cuenta la fórmula fundamental de la trigonometría. 
 Cuando el parámetro u recorre los valores del intervalo [0, 2p] el punto P recorre toda la circunferencia
1.-  Coloca el puntero del ratón sobre la escena, pulsa el botón izquierdo y con él pulsado desplaza el ratón y verás como se desplaza. Si pulsas el derecho y arrastras hacia arriba verás como se acerca, hacia abajo se aleja.
 
  Es muy importante que te acostumbres a utilizar las facilidades de interacción con la escena.

2.- Con los controles de la parte inferior de la escena puedes desplazar el punto  y aumentar o disminuir el radio
2. ECUACIONES PARAMÉTRICAS DE LA ELIPSE
Cuando estudiamos la elipse de centro el origen y semiejes a y b llegamos a la conclusión de que

es su ecuación reducida. Ahora vamos a demostrar que las ecuaciones:

nos determinan los puntos de la misma elipse. El procedimiento es el siguiente: elevamos al cuadrado ambas, dividimos la primera por a2 y la segunda por b2, sumamos estos resultados y aplicamos la fórmula fundamental de la trigonometría. Cuando el parámetro u recorre los valores del intervalo [0, 2p] el punto P recorre toda la elipse.
3.- Coloca el puntero del ratón sobre la escena, pulsa el botón izquierdo y con él pulsado desplaza el ratón y verás como se desplaza. Si pulsas el derecho y arrastras hacia arriba verás como se acerca, hacia abajo se aleja.
 
Usa los pulsadores de colores que tienen los controles
El botón Inicio restaura los valores iniciales.

4.-Con los controles de la parte inferior de la escena puedes desplazar el punto  y aumentar o disminuir los semiejes.

5.- Determinar las ecuaciones paramétricas cuando conocemos la forma explícita de la curva y=f(x) es muy sencillo. Tomamos x como parámetro y queda: 
       
Halla las ecuaciones paramétricas de una recta y las de una parábola (de eje vertical). Más difícil te resultará hallar las de una hipérbola. 
3. OTRAS CURVAS EN EL PLANO
Después de trabajar el ejercicio anterior podemos pulsar el botón que aparece  más abajo y nos aparecerá una escena  en la que podemos ver e interactuar con varias curvas del plano y familiarizarnos con sus ecuaciones paramétricas. 

6.- Debes observar todos los tipos de curvas que aparecen y en cada uno de los tipos obtener diversas curvas. Para ello modifica los  controles adecuados.

 
  Los controles que aparecen en la escena sirven para modificar las curvas y para cambiar de una curva a otra, pero no todos los controles actúan sobre todas las curvas. Las ecuaciones indican los que intervienen en cada una.
         
           
  Jesús Fernández Martín de los Santos
 
Ministerio de Educación, Cultura y Deporte. Año 2003
 
 

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.