
DISTRIBUCIONES BIDIMENSIONALES.
Si sobre una población de niños entre 0 y 6 años, estudiamos las variables peso y estatura, esperamos que en general ocurra que a mayor estatura también encontremos mayor peso, aunque es posible que en algunos pocos casos no ocurra así.
Vemos que existe una relación entre las dos variables, aunque no es funcional, o sea, no puedo determinar con exactitud el peso que corresponderá a cada talla.
En este tema trataremos de describir y medir este tipo de relaciones, que aparecen en gran cantidad de problemas.
Anota en tu cuaderno los conceptos que vas encontrando. Debes ser capaz de describirlos posteriormente.
DISTRIBUCIONES BIDIMENSIONALES
Cuando sobre una población estudiamos simultáneamente los valores de dos variables estadísticas, el conjunto de los pares de valores correspondientes a cada individuo se denomina distribución bidimensional.
Ejemplo 1:
Las notas de 10 alumnos en Matemáticas y en Lengua vienen dadas en la siguiente tabla:
|
MATEMÁTICAS |
2 |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
9 |
|
LENGUA |
2 |
2 |
5 |
6 |
5 |
7 |
5 |
8 |
7 |
10 |
Los pares de valores {(2,2),(4,2),(5,5),...;(8,7),(9,10)}, forman la distribución bidimensional.
Es frecuente que estudiemos sobre una misma población los valores de dos variables estadísticas distintas, con el fin de ver si existe alguna relación entre ellas, es decir, si los cambios en una de ellas influyen en los valores de la otra. Si ocurre esto decimos que las variables están correlacionadas o bien que hay correlación entre ellas.
En el ejemplo anterior parece que hay cierta tendencia a que cuanto mejor es la nota en Matemáticas, mejor es la de lengua.
NUBE DE PUNTOS O DIAGRAMA DE DISPERSIÓN
La primera forma de describir una distribución bidimensional es representar los pares de valores en el plano cartesiano. El gráfico obtenido recibe el nombre de nube de puntos o diagrama de dispersión.
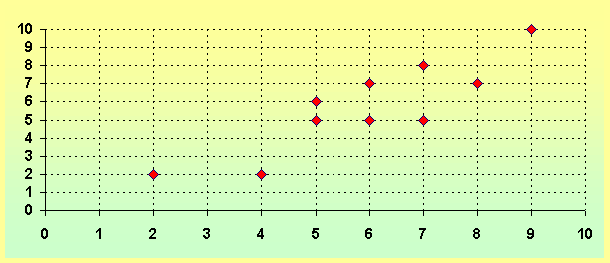
CORRELACIÓN LINEAL Y RECTA DE REGRESIÓN.
Cuando observamos una nube de puntos podemos apreciar si los puntos se agrupan cerca de alguna curva. Aquí nos limitaremos a ver si los puntos se distribuyen alrededor de una recta. Si así ocurre diremos que hay correlación lineal. La recta se denomina recta de regresión.
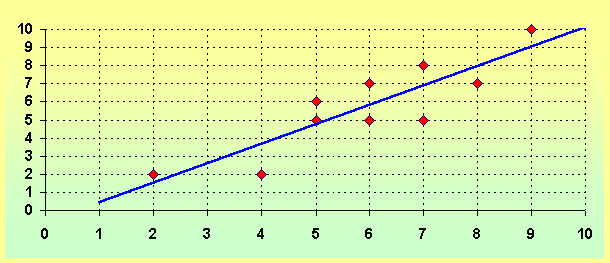
Hablaremos de correlación lineal fuerte cuando la nube se parezca mucho a una recta y será cada vez más débil (o menos fuerte) cuando la nube vaya desparramándose con respecto a la recta.
En el gráfico observamos que en nuestro ejemplo la correlación es bastante fuerte, ya que la recta que hemos dibujado está próxima a los puntos de la nube.
Cuando la recta es creciente la correlación es positiva o directa: al aumentar una variable, la otra tiene también tendencia a aumentar, como en el ejemplo anterior. Cuando la recta es decreciente la correlación es negativa o inversa: al aumentar una variable, la otra tiene tendencia a disminuir.
Ejemplo 2:
Una persona se entrena para obtener el carnet de conducir repitiendo un test de 50 preguntas. En la gráfica se describen el nº de errores que corresponden a los intentos realizados.
Observa que hay una correlación muy fuerte (los puntos están "casi" alineados) y negativa (la recta es decreciente).
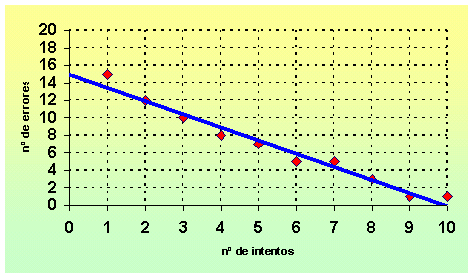
Ejemplo 3:
A 12 alumnos de un centro se les preguntó a qué distancia estaba su residencia del Instituto, con fin de estudiar si esta variable estaba relacionada con la nota media obtenida. Se obtuvieron los datos que figuran en la siguiente tabla:
|
Distancia (en km) |
0,05 |
0,1 |
0,12 |
0,4 |
0,5 |
0,7 |
1 |
1,2 |
2,1 |
2,5 |
3 |
3 |
|
Nota media |
8,4 |
4 |
5,7 |
9,1 |
6,3 |
6,7 |
4,3 |
5,4 |
7,8 |
4,5 |
7,2 |
8,1 |
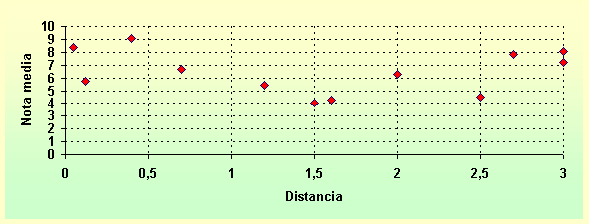
Observamos una nube de puntos que no nos sugiere ninguna recta concreta, porque la correlación es prácticamente inexistente, es decir, no tiene nada que ver con el rendimiento académico la distancia del domicilio al instituto,
La apreciación visual de la existencia de correlación no es suficiente.
Usaremos un parámetro, llamado coeficiente de correlación que denotaremos con la letra r, que nos permite valorar si ésta es fuerte o débil, positiva o negativa.El cálculo es una tarea mecánica, que podemos realizar con una calculadora o un programa informático. Nuestro interés está en saber interpretarlo.
Antes de ponernos a trabajar destacaremos una de sus propiedades
-1 < r < 1
A continuación tienes unos ejes con una nube de puntos que puedes modificar haciendo clic sobre ellos con el ratón y arrastrándolos. No tengas miedo de equivocarte, siempre puedes volver a la posición inicial pulsando el botón inicio. Las coordenadas de los puntos las puedes saber con aproximación naciendo clic en cualquier punto del plano y arrastrando hasta colocarte encima del punto.
Observa el valor de r, así como el ajuste de la nube a la recta. Intenta deducir las propiedades de r, relacionando su valor con la forma de la nube y realizando los siguientes ejercicios.
Acerca los puntos a la recta. ¿Hacia qué valor se aproxima r?
Aleja los puntos de la recta, separándolos entre sí ¿Hacia qué valor se aproxima r?
Mueve los puntos hasta que la recta tenga pendiente negativa, es decir, sea decreciente. En estas condiciones contesta a las preguntas anteriores.
Si alineas todos los puntos ¿Qué valor aproximadamente toma r?
Anota tus conclusiones en tu cuaderno; puedes ayudarte con el siguiente esquema:
|
Valor de r |
Tipo de correlación |
Nube de puntos |
| muy fuerte; fuerte; débil; muy débil; inversa; directa | ||
|
r>0 r próximo a 1 |
|
|
|
r>0 r próximo a 0 |
|
|
|
r< 0 r próximo a -1 |
|
|
|
r< 0 r próximo a 0 |
|
|
|
|r|=0,5 |
|
|
|
|r|=0,3 |
|
ESTIMACIÓN MEDIANTE LA RECTA DE REGRESIÓN
Es evidente que no todos dibujaríamos exactamente la misma recta para una nube de puntos, aunque la correlación fuera bastante fuerte.
De todas las rectas posibles los matemáticos han elegido como la mejor aproximación la llamada de los mínimos cuadráticos, Su cálculo es también algo mecánico que podemos hacer con calculadora o un ordenador. En el siguiente apartado encontrarás un ejercicio para estudiar sus propiedades.
La recta de regresión sirve para hacer estimaciones, teniendo en cuenta que:
Ejemplo 1:
Con los datos del primer ejemplo, (las notas de 10 alumnos en Matemáticas y en Lengua), podemos contestar con aproximación a la siguiente cuestión: si un alumno no realizó el examen de lengua, pero sí el de matemáticas, obteniendo un 7, ¿qué nota cabe esperar que obtuviera en lengua?
|
MATEMÁTICAS |
2 |
4 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
9 |
|
LENGUA |
2 |
2 |
5 |
6 |
5 |
7 |
5 |
8 |
7 |
10 |
Observa el punto amarillo, cuya abscisa corresponde a la nota de matemáticas y su ordenada a la nota que esperamos que tenga en lengua. Es resultado es aproximado y relativamente fiable, ya que la correlación es fuerte Y el valor de la nota no está muy próximo a la media, aunque el nº de datos que tenemos no es muy alto.
Puedes cambiar el valor de la nota de matemáticas sin más que cambiar su valor en el recuadro de la parte inferior.
PROPIEDADES DE LA RECTA DE REGRESIÓN DE LOS MÍNIMOS CUADRÁTICOS.
En la siguiente escena puedes comprobar las principales propiedades de la recta de regresión mínimo-cuadrática.
Observa la recta blanca, cuyos coeficientes a y b puedes hacer variar en los recuadros inferiores de la escena, bien con las flechas o introduciendo los valores deseados. Observa los segmentos denominados di, que marcan las distancias de los puntos de la nube a la recta en la dirección del eje OY.
Haz variar los valores de a y de b. Cuando la recta coincida con la recta de regresión mínimo-cuadrática (en color azul claro) la suma de los cuadrados de las distancias di es la mínima posible.
Observa el punto P(p,q), cuyas coordenadas puedes hacer variar en los recuadros correspondientes de la parte inferior de la escena. Observa lo que ocurre si le das a p y a q los valores de las medias de la distribución (puedes escribir mx en la casilla de p y pulsar intro y escribir my en la casilla de q y pulsar intro). Mueve ahora los puntos rojos y repite el ejercicio. ¿qué propiedad puedes deducir?
Autora: Celia Berrocal Sánchez
| Ministerio de Educación, Cultura y Deporte. Año 2001 | ||