CÁLCULO APROXIMADO DE ÁREAS BAJO UNA CURVA:

MÉTODO DE LOS TRAPECIOS

Área del trapecio.

1.- Dibuja en tu cuaderno la figura siguiente:

Calcula el área del trapecio limitado por:

• la gráfica de la función
• el eje OX
• las rectas x = a , x = b

Si la función representada corresponde a la velocidad en m/s de un móvil a lo largo del tiempo, ¿qué representa el área calculada?

Área bajo una poligonal

2.- Dibuja en cada caso los recintos limitados según se indica, asociados a la gráfica de la siguiente función poligonal, y calcula su área.

• Región limitada por la gráfica de la función, el eje OX y las rectas x = 0 , x = 2.
• Región limitada por la gráfica de la función, el eje OX y las rectas x = 2 , x = 5.
• Región limitada por la gráfica de la función, el eje OX y las rectas x = 0 , x = 5.
• Región limitada por la gráfica de la función, el eje OX y las rectas x = 5 , x = 13.
• Región limitada por la gráfica de la función, el eje OX y las rectas x = 0 , x = 13.

Área bajo una función por descomposición en figuras conocidas.

3.- Halla el área de la zona sombreada teniendo en cuenta que ahora la función está formada por cuadrantes de circunferencia y segmentos.

El problema del área bajo una curva.

Las dificultades empiezan cuando hay que calcular el área de la región determinada por la gráfica de una función cualquiera, y = f(x), el eje OX, y dos rectas paralelas al eje OY: x = a, x = b, como en el caso de la figura siguiente:

Nos vamos a conformar con obtener un valor aproximado. Para ello, trazamos el segmento que une los puntos extremos de la gráfica y hallamos el área del trapecio que determina.

4.- Calcula el área aproximada del recinto limitado por la gráfica de la función y = f(x), el eje de abscisas y las rectas x = 0 y x = 12 , mediante el trapecio correspondiente.

5.- Observa la figura y decide, en cada uno de los casos siguientes, si el área real es mayor o menor que el área aproximada:

a = 0 , b = 11
a = 2 , b = 11
a = 2 , b = 9
a = 4 , b = 9
a = 4 , b = 7

(Para modificar los valores de a y b, puedes utilizar las flechas de colores o escribir directamente los valores en las celdas y pulsar Enter. El botón Inicio presenta las condiciones de partida.)

6.- Cambia los valores de a y b de forma que difieran cada vez menos y observa cómo el segmento se aproxima cada vez más a la gráfica de la función.

Área aproximada bajo una curva mediante trapecios

Para aproximar mejor la función, consideramos la partición del intervalo [0,12] en 4 partes iguales y unimos los puntos correspondientes de la gráfica mediante segmentos.

Así obtenemos 4 trapecios, como se ve en la figura.

La suma de sus áreas es:

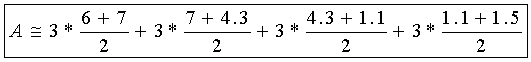
Como las divisiones del intervalo son iguales, podemos sacar factor común su longitud, 3 , y obtenemos :

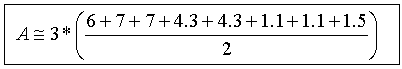
Y operando:

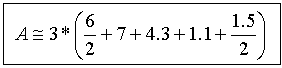
Con lo que se obtiene fácilmente un valor aproximado del área :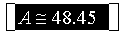

7.- Dibuja la figura que se obtiene dividiendo el intervalo [0,12] en 10 partes iguales y halla el área aproximada del recinto por el método de los trapecios.

(Puedes ver las coordenadas de cualquier punto situando el ratón sobre él y pulsando el botón principal).

8.- Halla el área aproximada del recinto limitado por la gráfica de la función 

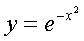
y el eje OX, dividiendo el intervalo correspondiente en 10 partes iguales y aplicando el método de los trapecios.

Autora: Mª del Amor Pastor