El rectángulo de Harry Langman (New York)
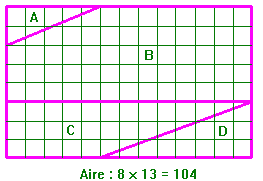
El rectángulo de Harry Langman (New York)

Curioso,
las figuras parecen compuestas de los mismos trozos.
Sin
embargo no tienen el mismo área.
¿Dónde
está el problema?
![]() Solution
Solution
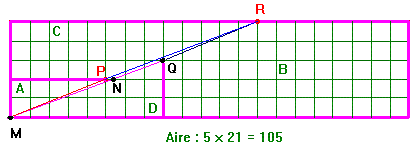
Miremos bien la figura : los puntos P y N no están confundidos contrariamente se puede pensar en la figura reconstituida. La figura C es de hecho el polígono limitado por PR y no NR. Del mismo modo la figura A está limitada por MP y no MN. La figura B está limitada por QR y D por MQ que pasa por N.
Tenemos pues un agujero constituido del polígono MPRQN cuyo área es exactamente igual a una unidad. Como esta unidad está dispersada en longitud seguramente es casi invisible.
Se puede también explicar el resultado observando que los puntos M, P y R no están alineados. Era pues un error de reconstitución. Es difícil verlo (desplaza la recta de encima), ya que de hecho los segmentos MP y QR son paralelos pero con PQ...lo que resulta aberrante.Volvemos a encontrarnos una vez más, los números 5, 8, 13, 21 que forman parte de la sucesión de Fibonacci. Si elegimos dos números consecutivos de la sucesión para longitud y anchura de un rectángulo y los que lo encuadran para el otro rectángulo, obtenemos alternativamente una ganancia o una pérdida de 1 unidad.
Estas ganancias y pérdidas se traducen por la formación o la superposición de un ligero espacio vacío tan pequeño como grandes sean los números.