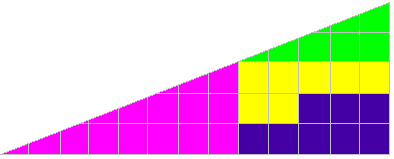
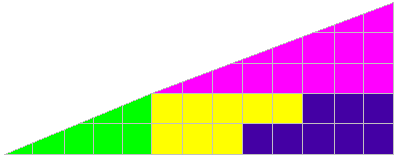
El triángulo de Gardner

Una vez más, hay truco y seguramente es casi invisible. Las dos figuras son cuadriláteros y no triángulos.
En realidad hemos ganado una unidad cerca de "la oblicua" de la segunda figura. Esta "oblicua" no es una línea recta.
Para obtener una línea recta la relación 2/5 de los lados del ángulo recto del triángulo verde tendría que ser igual a la relación correspondiente 3/8 en el triángulo rosa. Pero 2/5 es distinto que 3/8 . Lo que se traduce en un ligero hueco en la figura de arriba y en un ligero arqueado en la segunda. La primera figura es un cuadrilátero cóncavo y la segunda un cuadrilátero convexo. La diferencia es tan pequeña cerca de "la oblicua" con respecto a la superficie total que es difícil percibirlo. Está repartida en longitud y corresponde exactamente a una unidad.
Haz descender con el ratón la recta de encima y veras que "la oblicua" no es una recta..
¡El juego está echado!
La sucesión de Fibonacci está siempre ahí con los números: 2,3,5,8,13... que aparecen como longitudes de los lados.