Las orejas de burro

Las orejas Solución

 

Las orejas
El profe, pone un problema en su clase:
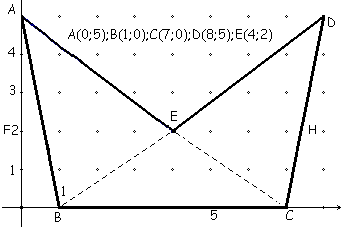
       Se trata de calcular el área de las orejas de burro de aquí abajo con las coordenadas de los puntos A, B, C, D, E señalados sobre la figura.
       ¡Es  muy sencillo cuando se sabe calcular el área de un trapecio o de un triángulo!.
       Cada cual se dedica a trabajar con su método y finalmente obtenemos los resultados siguientes:

 

Primer método: cálculo de la diferencia de las áreas del trapecio (ABCD) y del triángulo (AED).
        Área (ABCD) - Área (AED) =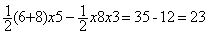

Segundo método: cálculo directo.
        Área (ABC) + Área (BDC) - Área (BEC) =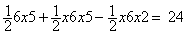

Cada uno de los dos métodos parece exacto, sin embargo los resultados son diferentes.
¿Hay  algún resultado bueno?
Si es que sí, ¿cuál es el bueno?. Y entonces, ¿dónde está el error ?

Solución 

Los dos procedimientos parecen exactos a priori.
Pero el segundo procedimiento utiliza la alineación de los puntos A, E y C, como la simétrica de los puntos D, E y B.
Y estos puntos no están alineados. En efecto, si lo estuvieran tendríamos una igualdad para las tangentes de los ángulos AEF y HEC.
       Pero tangente(AEF) = 3/4
       y tangente(HEC) = 2/3
       y 3/4 2/3.
Se puede verificar que la recta (AC) no pasa por E, poniendo el ratón sobre la figura de abajo.

Mediante el cálculo se verifica bien que el punto de intersección de las dos rectas (AC) y (BD) no es E:
(AC) de ecuación y = -(5/7) x + 5 y
(BD) de ecuación y = (5/7) x + - 5/7
tienen como intersección el punto de abscisa x =4 y de ordenada y =15/7.

 

Así pues el resultado exacto es el primero que utiliza la diferencia de área del trapecio y la del triángulo sin hacer intervenir las rectas (AC) y (BD): es 23.