La historia de las matemáticas ha sido precedida de una larga prehistoria de la que tenemos algunos trazos que se remontan a 4000 años. Los animales superiores y los niños perciben en nuestro mundo dos entidades abstractas fundamentales: el número y la forma. La aritmética y la geometría fueron de este modo, durante mucho tiempo distintas, las dos ciencias fundamentales. En un principio el conocimiento de los números por el hombre no  fue muy fino. El hombre, en las sociedades primitivas, no distinguía entre dos conjuntos equipotentes (con el mismo número de elementos), apenas sabía contar: uno, dos, muchos. "Muchos" se dice "tres" en latín: esta palabra subsiste todavía hoy en francés: "très", pero también "trois".

El sistema más antiguo consistía en contar con los dedos. ¿Pero cómo anotar el resultado?	Después contaron y anotaron grandes números echando fichas en una bolsa.	Se dieron cuenta entonces de que bastaban    unas simples marcas grabadas sobre una tablilla.	Los Babilonios utilizaron marcas de formas diferentes para designar grandes números.	Diversos símbolos colocados en diferentes posiciones bastaban para representar los números más grandes.

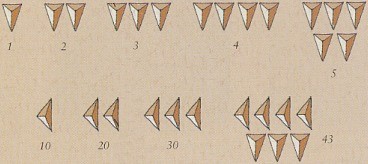
Notaciones a lo largo de las épocas :

Las civilizaciones más antiguas observaban las vueltas a la redonda de los astros en el cielo. Sabemos así que los Sumerios de Uruk y de Nippur (- 3000) utilizaban ya un calendario lunar. Y que tuvieron la idea de representar los números por símbolos: la luna representaba la unidad, lunas juntas los números siguientes. La necesidad de hacer cuentas y de escribirlas les condujo a utilizar abreviaciones más cómodas. La barra vertical u oblicua tiene entonces sentido de unidad (Fenicios, Sirios, Nabateos, Griegos antiguos, Árabes del sur, Hindúes). Los conjuntos de cinco, diez o veinte unidades eran abreviados por símbolos especiales, eventualmente derivados de su nombre. Todos estos sistemas eran aditivos, es decir el número código es la suma de los símbolos representados.

Los Babilonios (- 2000) se destacan al inventar el sistema sexagesimal: los símbolos de base valen 1, 10, 60, luego 600, 3600, 36000 y así sucesivamente. Este sistema se ha perpetuado hasta nosotros, mediante la astronomía, para las medidas sexagesimales de tiempos y de ángulos.

Fuente : G. IFRAH Historia universal de las cifras.

Tablilla sumeria que data alrededor del 2000  antes de nuestra era. Describe un recuento del ganado por medio de signos y cifras cuneiformes.

Fuente : G. IFRAH Historia universal de las cifras.

Tablilla contemporánea de la precedente proveniente de una hoja clandestina en Tello.

Varias civilizaciones han tenido además, la idea de utilizar las letras de su alfabeto para representar los números. Esto permite dar un sentido a algunos de entre ellos: son los cálculos cabalísticos. El número correspondiente a una letra viene a ser función de la posición de ésta en la palabra; la necesidad de marcar la "nada" se hace sentir. El origen del cero todavía permanece oscuro. Con toda seguridad existe en textos Hindúes del siglo VI donde toma la forma de un punto. En escritos astronómicos griegos, el cero está representado por la letra o inicial de la palabra griega omdem : "nada".
Los hindúes llamaban al cero: sunya,  es decir "el vacío". Traducido al árabe esto dió sifr, que traducido al latín algunos siglos más tarde dió zefiro. Se olvidó el fi y se obtuvo zéro en francés y cero en español. Este sifr finalmente designó la colección entera de los símbolos que permiten escribir los números, las cifras: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

No puede haber números negativos sin cero. Ni los calculadores Babilonios o Egipcios, ni los pensadores griegos o después de ellos los matemáticos árabes, dispusieron de la noción general de números negativos. Los primeros que utilizaron cantidades negativas fueron los matemáticos hindúes, particularmente Bramagupta, quienes desde el siglo VII las utilizaron para necesidades contables. Los bienes estaban representados por números positivos y las deudas se inscribían como cantidades negativas.
Habrá que llegar a finales del siglo XV  para ver aparecer en Occidente seres numéricos no positivos... Se establecieron reglas de utilización de estos seres: la regla de los signos. Sin embargo se les negó la existencia en tanto que seres reales, y por tanto como números. Son designados por numeri absurdi. Incluso Descartes más tarde (1596-1650) designa una raíz no positiva de una ecuación como una raíz falsa. Carnot (1753-1823) escribe : "Para obtener realmente una cantidad negativa aislada, habría que sustraer una cantidad efectiva de cero: operación imposible. ¿Cómo concebir pues una cantidad negativa aislada?".

La forma actual de nuestras cifras, nuestro sistema decimal, viene pues de la India del Oeste, por mediación de los Árabes. Pero no es hasta el siglo XIII cuando penetró en Italia, adoptada por los comerciantes de Florencia. Su empleo no se generalizó hasta el siglo XVI

Es la invención de la imprenta (1440), la que fija finalmente la forma de estos diez símbolos. El uso de la coma para anotar los números "reales" no se extiende hasta el siglo XVII.

Las cuatro operaciones son conocidas ya por los Egipcios.
He aquí la multiplicación egipcia de 37 par 24 : (para más explicaciones ver la multiplicación egipcia )

Un bastón vale 1 unidad. Un hueso vale 10 unidades . Una espiral vale 100 unidades. La flor de loto vale 1000 unidades. El resultado final está escrito a la izquierda.

Pero sus representaciones son a menudo incomodas.
La yuxtaposición marca la adición y una y girada marca para los griegos, la sustracción.

Finalmente, son los copistas de la Edad Media quienes abrevian y luego deforman la palabra "y", que se convierte "+", mientras que la costumbre de separar en las cuentas el peso de la tara con ayuda de una raya horizontal da lugar al nacimiento del signo "-". Los signos "+" y "-" aparecen en la Aritmética comercial de Widmann en 1489. Los signos de multiplicación y de división actuales no son introducidos hasta el siglo XVII. La igualdad está marcada en Europa en el siglo XVII por el símbolo ,por el cual los astrónomos designan la constelación del Toro, pero también encontramos la palabra latina "aequalis" con todas letras, y es abreviada progresivamente en æ hasta convertirse, finalmente, en el signo "=". parece haber sido inventado por el matemático inglés Robert Recorde (1510-1558), profesor en Oxford y en Londres. El símbolo designa por entonces el número 1000. Y será J. Wallis quien, hacia 1660, lo eleva al rango de "infinito"; anteriormente, esta noción de infinito no tenía existencia.

Conclusión :
¡La humanidad ha invertido varios miles de años en domesticar al número, y la ciencia ha llegado a ser lo que es después de algunos siglos!
Las matemáticas no se han hecho en un día y, es más, su infancia apenas está alejada de nosotros. ¿Qué tiene de extraño entonces, puesto que los hombres han tardado tanto tiempo en representar los números y las operaciones, que un estudiante encuentre algunas dificultades en este tema?

 

Los Mayas, civilización meso-americana cuyo apogeo se sitúa entre 250 y 950 de nuestra era, contaban en base veinte.

 

         

 

 

(1)
Résolution de problèmes par l'homme et la machine de J.L Laurière
Histoire des mathématiques pour les collèges (ed CEDIC)
Historia universal de las cifras de Georges Ifrah. EDITORIAL ESPASA CALPE