La banda de Möbius
"El asombro es la sal de la tierra." M.C.Escher

Imagina una superficie en la que las dos caras se convierten en una sola; llegarás al otro lado sin cambiar nunca de cara y sin atravesar el borde. Es la banda de Möbius. Coge una larga cinta de papel y une los extremos después de haber dado media vuelta con uno de ellos tal como se indica aquí al lado. Tienes una banda de Möbius, apellido de Augusto Möbius, que publicó una construcción sobre ella en 1865.

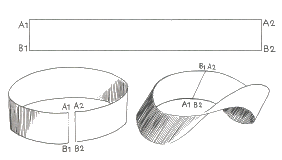
Sigue la mosca... la banda no tiene más que un solo borde.

Si de un punto cualquiera trazamos una línea en una dirección no pasando por el borde, nos encontramos a mitad de camino con el punto de partida, pero en el otro lado del papel. Continuamos y nos volveremos a encontrar entonces con el punto de partida, en el mismo lado.

Sigue la mosca... la banda no tiene más que una sola cara.

Como no tiene más que una cara, una cinta transportadora a la que le se habría dado media vuelta estará usada de forma regular por los dos lados.
Varias marcas de imprenta matricial utilizaban casetes con una banda de Möbius. La banda estaba tintada por los 'dos' lados. El pliegue de la banda era puesto en marcha por una lengüeta de plástico situada justo antes de su salida.
Algunas personas bastante ingeniosas volvían a poner tinta en esta banda hasta una decena de veces, con una tinta de calidad, buenos guantes y sobre todo una buena dosis de buen hacer.
Muchos usuarios ignoraban evidentemente que su casete era una banda de Möbius.

Se puede extender una banda cilíndrica (dos caras y dos bordes) entre dos rodillos. Para la banda de Möbius (una sola cara y un solo borde) hacen falta tres.

Si cortamos ahora esta banda por su línea mediana, no obtenemos dos trozos sino uno solo, formando cuatro medias vueltas como si a los extremos de la banda les hubiéramos dado dos vueltas completas antes de haberlos juntado. Los bordes forman ahora dos curvas distintas, es decir ya no hay un solo borde ni una sola cara, y por tanto ya no será una banda de Möbius sino una banda cilíndrica.

Sigue la mosca... no hay más que una sola banda.

La botella de Klein es una superficie cerrada con una sola cara; no admite ni interior ni exterior y no está orientada. De forma imaginaria, podríamos obtener esta superficie estirando el cuello de una botella y enlazándolo por el interior con el fondo, después de haberle hecho atravesar la botella. La banda y la botella tienen una íntima relación, que se podría ver si cortásemos la botella en dos de arriba a abajo, pues la mitad de una botella de Klein sería una banda de Möbius. (Dictionario de las matemáticas de A. Bouvier, M. Georges et F. Le Lionnais.)