Gogora ezazu garrantzitsuena
  • Funtzioa x eta y aldagaien arteko erlazioa da, era horretan aldagai independenteari, x-ri, egokitzen zaio aldagai dependentearen, y-ren, balio bakarra.
  • Funtzio baten eremua x-ek har ditzakeen balio posible guztien multzoa da.
  • Funtzio baten grafikoa planoan irudikatzen diren puntuen multzoa da, (x,f(x)).
  • Funtzioa jarraia da marra batez irudika badaiteke. Puntu batean etena da, "jauzi" bat baldin badauka edo puntu horretan definituta ez badago.
  • Funtzioa periodikoa da, t periodoaz, grafikoa t unitate bakoitzean errepikatzen bada, f(x+t)=f(x).
  • Funtzio bat simetrikoa da OY ardatzarekiko, baldin eta f(-x)=f(x). eta simetrikoa da jatorriarekiko, funtzio bakoitia, baldin eta f(-x)=-f(x).
  • Funtzio baten bi punturen arteko aldakuntza-tasa (TV) ondoko diferentzia da: AT [x1,x2]=f(x2)-f(x1)
    Batez besteko aldakuntza-tasa (TVM) da:
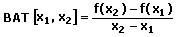
  • Funtzio bat tarte batean gorakorra da, bertako edozein bi puntu emanda
    • Baldin eta x1<x2 orduan f(x1)<f(x2)
    Eta beherakorra da
    • Baldin eta x1<x2 orduan f(x1)f(x2)
  • Funtzio jarrai batek x=a puntuan, maximo erlatiboa dauka, puntu horren ezkerraldean gorakorra bada eta eskuinaldean beherakorra. Aldiz, lehenengo beherakorra bada eta gero gorakorra, minimo erlatiboa dago.
  • Funtzio baten grafikoa ahurra (beherantza) edo ganbila (gorantza) izan daiteke. Ahurtasuna aldatzen den eremuko puntuei inflexio-puntuak deitzen zaie.
aurrekoa
hurrengoa