APLICACIONES DE LA DERIVADA

PROBLEMAS DE OPTIMIZACIÓN

 

Ejemplos

Problemas de optimización

En numerosas ocasiones nos interesa conocer sólo el máximo o el mínimo de una función. Estos problemas a menudo requieren un planteamiento previo que, resumiendo, es el siguiente:

  1. Determinar la función de la que se quiere obtener el máximo o el mínimo.
    Es fácil que ésta dependa de más de una variable.
    Si hay más de una variable, buscar la relación entre ellas para que la función sólo dependa de una incógnita.

  2. Calcular el máximo o el mínimo pedido, imponiendo las condiciones necesarias en sus derivadas.

  3. Criticar la solución obtenida

 

Veamos unos ejemplos:

Una empresa ha decidido mejorar su seguridad instalando 9 alarmas. Un especialista en el tema señala que dada la estructura de la empresa sólo puede optar por dos tipos de alarmas, de tipo A o de tipo B; además, afirma que la seguridad de la empresa se puede expresar como la décima parte del producto entre el número de alarmas de tipo A instaladas y el cuadrado del número de alarmas instaladas de tipo B. ¿Cuántas alarmas de cada tipo se deben instalar en la empresa para maximizar su seguridad?.

a. Determinar la función

  • Llamemos x a las alarmas de tipo B instaladas, con lo que las alarmas de tipo A serán (9-x)

  • La seguridad de la empresa viene expresada por la función f(x)=(9-x)x2/10=(9x2-x3)/10

b. Calcular el máximo

  • Calculamos f'(x)=(18x-3x2)/10  

  • Resolvemos la ecuación: f'(x)=0. Soluciones: x=0, x=6

  • Calculamos f''(x)=(18-6x)/10 y  su signo en estos valores. El máximo se obtiene en x=6

c. Criticar las soluciones

  • Deberemos instalar 6 alarmas de tipo B y 3 de tipo A

 

 

A un lado de un río de 1 km de anchura hay una central eléctrica y al otro lado, 8 km corriente arriba, una factoría. Tender un cable por tierra cuesta 3 pts/metro y bajo el agua 5 pts/metro. ¿Cuál es el tendido más económico desde la central a la factoría?.

a. Determinar la función

  • Observa la escena, sea P el punto en que el cable comienza a estar bajo el agua y 8-x la distancia entre el punto P y la central C, la distancia entre P y la factoría F será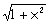

  • Precio del tendido: 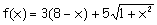miles de ptas

b. Calcular el mínimo

  • Calculamos

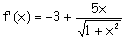
  • Resolvemos la ecuación: f'(x)=0.

    • Soluciones: x=0,75, x=-0,75 (observa que la solución negativa no tiene sentido en este caso)

  • Calculamos f''(x)  y  su signo en éste valor comprobando que efectivamente hay mínimo en x=0,75

c. Criticar las soluciones

  • El tendido más económico se obtiene haciendo que el cable cruce el río a 7,25 km de la central, o por simetría, de la factoría, siendo el coste mínimo 28000 ptas.

 

EJERCICIOS DE APLICACIÓN

1. La suma de un número y el doble de otro es 7,5. Calcula dichos números para que: 

a) La suma de sus cuadrados sea mínima

  • Llamemos x a uno de los números el otro será (7,5-2x)

  • La función a minimizar será f(x)=x2+(7,5-2x)2

  • Calcula f'(x) y resuelve la ecuación: f'(x)=0

  • Calcula f''(x) y  su signo en estos valores

  • Introduce las expresiones de f'(x) y de f''(x) en la escena para comprobar el resultado

  • ¿Qué números son?
b) La diferencia de sus cuadrados sea máxima.

  • Procede igual que antes pero dando al parámetro a el valor -1

 

2. Considera un rectángulo de perímetro p y área a,

a) Si el perímetro es 8, calcula sus dimensiones para que el área sea máxima

  • Observa las incógnitas en la escena y escribe la función a maximizar y=f(x)

  • Calcula f'(x) y resuelve la ecuación: f'(x)=0

  • Calcula f''(x) y  su signo en estos valores

  • Para comprobar el resultado introduce el valor de f'(x) y de f''(x) en la escena

  • ¿En qué puntos corta f'(x) al eje OX?. ¿Cómo es f''(x) en este punto?

  • Si cambias el valor de x se dibujará
    y=f(x) y podrás observar su comportamiento.

b) Si el área es 4, calcula las dimensiones del que tiene perímetro mínimo

  • ¿Cuál es ahora la función a maximizar y=f(x)?

  • Calcula f'(x) y resuelve la ecuación: f'(x)=0

  • Calcula f''(x) y  su signo en estos valores

  • Para comprobar el resultado introduce el valor de f'(x) y de f''(x) en la escena

  • ¿En qué puntos corta f'(x) al eje OX?. ¿Las dos soluciones son válidas en este caso?. ¿Cómo es f''(x) en estos puntos?

  • Si cambias el valor de x se dibujará
    y=f(x) y observarás su comportamiento.

 

 

3. El coste total de producir x unidades de un determinado producto es  C(x)=9-2x+x3/6 y cada unidad se vende a (12-3x) unidades monetarias,

a) Calcula cuántas unidades se deben producir para que el coste medio por unidad sea mínimo.

  • Escribe la función a minimizar, f(x)=C(x)/x

  • Calcula f'(x) y resuelve la ecuación: f'(x)=0  

  • Calcula f''(x) para los valores obtenidos

    • Para comprobar el resultado introduce el valor de f'(x) y de f''(x) en la escena.

    • ¿En qué puntos corta f'(x) al eje OX?.

    • ¿Cómo es f''(x) en estos puntos?

    • Si cambias el valor de x se dibujará y=f(x) y podrás observar su comportamiento.

b) Calcula cuántas unidades se deben vender para que el beneficio sea máximo

  • Escribe la función y=g(x)
    beneficio=ingresos-costes

  • Calcula g'(x) y resuelve la ecuación: g'(x)=0

  • Calcula g''(x) y  su signo en estos valores

  • Para comprobar el resultado introduce el valor de g'(x) y de g''(x) en la escena

  • ¿En qué puntos corta g'(x) al eje OX?. ¿Las dos soluciones son válidas en este caso?. ¿Cómo es g''(x) en estos puntos?

  • Si cambias el valor de x se dibujará
    y=g(x)     y verás su comportamiento.

 

María José García Cebrian