VECTORES
 
Volver al índice
11.- Producto escalar de dos vectores
 
u . v = |u| . |v| . cos (u,v)
Producto de sus módulos por el coseno del ángulo que forman
¡Atención! |u|, |v| y cos(u,v) son números. El producto u.v es un número. De ahí le viene el nombre, pues escalar significa número. O sea el resultado del producto escalar de dos vectores NO ES UN VECTOR, ES UN NÚMERO.

NOTA: A partir de ahora vamos a considerar siempre que las coordenadas de todos los vectores están referidas a la base ortonormal B(x,y), siendo las componentes de x(1,0) y las de y(0,1)
 
En la escena siguiente puedes mover con el ratón los extremos de los vectores u y v, verás como va cambiando el |u|, el |v|, el ángulo que forman A, y su coseno. Por último verás el producto escalar de los dos vectores, o sea u.v

Volver al índice


12.- Propiedades del producto escalar
1.- Comprueba que si u=0 o v=0, u.v=0 

2.- Comprueba que si u es perpendicular a v, u.v=0, siendo u ¹ 0 y v ¹ 0, pues entonces A=90º, y el cos90º=0 

3.- Propiedad conmutativa 
u.v = v.u  

4.- Propiedad asociativa 
a(u.v) = (au).v 
 a=número 
u=vector 
v=vector
 
5.- En una base ortonormal B(x,y) o sea x=(1,0) y=(0,1) 
se cumple
 
x.x = 1
 Para comprobarlo pones en la escena anterior 
u = x = (1,0)      v = x = (1,0)
y.y = 1
 Para comprobarlo pones en la escena anterior 
u = y = (0,1)      v = y = (0,1)
x.y = y.x = 0 Para comprobarlo pones en la escena anterior 
u = x = (1,0)      v = y = (1,0)
 
 
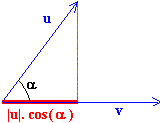
6.- v.u = |v|.(|u|.cos (a)) = |v|.(proyección de u sobre v) 
de donde proyección de u sobre v = 
 
7.- Propiedad distributiva:
u. (v + w) = u.v + u.w
 
 
Moviendo los extremos de los vectores u, v y w, podrás comprobar esta propiedad
 
Volver al índice


13.- Expresión analítica del producto escalar

Si las coordenadas de los vectores u y v respecto a una base ortonormal son:

                                                            u (u1,u2)      v(v1,v2)

 
 
el producto escalar queda así:
 u.v = u1.v1 + u2.v2
 
Podrás comprobarlo en la escena siguiente, moviendo los extremos de los vectores u y v (o cambiando los valores de las coordenadas en los botones inferiores),  viendo el valor de sus coordenadas y de su producto escalar u.v

EJERCICIO 13

Comprueba las propiedades 1 y 2 del producto escalar:
1.- Mueve el extremo de u hasta que sus coordenadas sean (0,0), o bien introduce los valores (0,0) en los botones inferiores de la escena, para comprobar la propiedad 1. 

2.- Después de dar al botón inicio, anota en tu cuaderno las coordenadas de u y v y las operaciones necesarias para obtener el producto escalar u.v 
3.- Con los botones inferiores de la escena, cambia las coordenadas de los vectores para que sean perpendiculares. 

4.- Anota en tu cuaderno las coordenadas elegidas y el cálculo del producto escalar u.v
 

Volver al índice 

14.- Módulo de un vector en función de sus coordenadas
 
v.v = |v|.|v|.cos (v,v) = |v|2.cos 0 = |v|2.1 = |v|2
Por tanto: 
Si las coordenadas de v son (v1,v2)
v.v = v1.v1 + v2.v2 = v12 + v22
 
 Volver al índice 

15.- Coseno del ángulo de dos vectores
 
De la definición de producto escalar: 
u.v = |u|.|v|.cos(u,v)
se deduce que: 
  Y mediante las coordenadas:
EJERCICIO 14

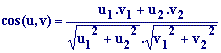Con los vectores u y v de la escena del EJERCICIO 13 ya vimos cuánto valía u.v, calcula ahora en tu cuaderno:
1.- |u|

2.- |v|

3.- cos (u,v) y el ángulo (u,v)

4.- ¿Cuánto tiene que valer x para quev(x,2) sea ortogonal a u? Observa la relación entre las coordenadas de u y éste vector ortogonal a él.


Las soluciones a este ejercicio las puedes comprobar en la escena siguiente:
 
 Volver al índice 
Autora: Ángela Núñez Castaín
 
Ministerio de Educación, Cultura y Deporte. Año 2000