
LÍMITE, CONTINUIDAD Y DERIVABILIDAD EN FUNCIONES A TROZOS
En las siguientes escenas vamos a comprobar los conceptos de límite, continuidad y derivabilidad. Se proponen unos ejercicios que debes contestar por escrito en tu cuaderno.
Límite de una función en un punto. Continuidad y clasificación de discontinuidades.
Actividad 1.
Consideremos la siguiente función f(x) definida a trozos:
En la siguiente escena está representada la función. Pincha con el ratón en el valor de la abcisa y teclea 1.6. Observa que hay un punto azul sobre la curva. En la parte inferior derecha puedes comprobar las coordenadas del punto.
a) Construye una tabla para valores de x cada vez más próximos a -2 por la izquierda (-2.1, -2.01, -2.001,...) y otra para valores cada vez más próximos a -2 por la derecha. Compara los resultados con el valor de f(-2). b) Expresa en lenguaje matemático (con límites) estos resultados. ¿Qué tipo de discontinuidad hay en x=-2?
c) ¿Qué otras discontinuidades hay en esta función? ¿Por qué? Utiliza lenguaje matemático.
d) ¿Por qué es continua en x=4?
Habrás observado que las posibles discontinuidades de una función definida a trozos están en los punto que separan cada trozo.
Actividad 2.
Consideremos ahora la siguiente función:
En la siguiente escena está representada la función para a=0, b=0 y k=1. Queremos hallar a, b y k para que sea continua en todos sus puntos. Se puede arrastrar con el ratón el punto (-2,1); observa como cambia la expresión de f(x).
a) ¿Existe el límite cuando x tiende a -2 de f(x)? Observa que f(-2)=k. ¿Cuál es el valor de k para que f sea continua en x=-2? b) Busca tres rectas para x>1 de modo que f(x) sea continua en x=1 (tres valores para
a y b).c) Comprueba, usando límites, la continuidad en x=1 para los tres casos del apartado anterior.
Podemos "pegar" un trozo de función con una semirrecta: "pegar" significa que la función resultante sea continua.
En esta escena puedes ensayar la función definida a trozos que tú te inventes. Para ello tienes que cambiar, en la parte inferior, el valor 0 que aparece en la expresión "y=f(x)*(0)" por la expresión que creas conveniente; y lo mismo en "y=g(x)*(0)". No tiene gracia sustituir 0 en las dos sitios con la misma expresión. (Si quieres indicar un producto se usa "*")
| a) Busca la
expresión de una función f(x) definida a
trozos que tenga una discontinuidad evitable en x=-1,
sabiendo que f(-1)=2. b) Busca la expresión de una función c) Busca la expresión de una función h(x) definida a trozos que tenga una discontinuadad de salto (finito o infinito) en x=-1, sabiendo que h(-1)=2. |
Podemos "pegar" dos trozos de funciones: "pegar" significa que la función resultante sea continua.
Derivabilidad.
Recuerda:
Consideramos la función
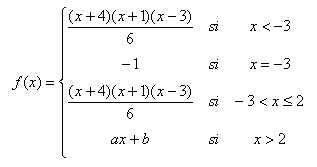
En la siguiente escena está representada la función para a=0 y b=0. Queremos hallar a y b para que sea derivable en todos sus puntos salvo en x=-3. Modificando xo puedes moverte por los puntos de la curva (las coordenadas del punto aparecen abajo a la derecha en azul claro). Para cada punto P aparece dibujada la recta tangente y la pendiente m (abajo a la derecha).
| a) ¿Por qué no es derivable en x=-3
(no aparece la recta tangente)? b) Escribe la ecuación de la recta tangente en x=-1 y en x=1. c) Modifica a y b para que f(x) sea derivable en x=2. Para facilitar la solución, aparecerá dibujada la recta tangente en x=2 pero no el valor de m: este valor aparece si encuentras la solución. d) En la función f(x) para x>2, en vez de la recta ax+b, deseo que aparezca una curva. ¿Puedes escribir la expresión de esta nueva f(x)? (Ya no te sirve la escena) |
Podemos "pegar bien" dos trozos de funciones: "pegar bien" significa que la función resultante sea continua y derivable. Esta idea se puede ampliar y hablar de "pegar doblemente bien", "pegar triplemente bien", ...: "pegar doblemente bien" significa que la función resultante sea continua y dos veces derivable, ...
Autor: Juan Simón Santamaría.
| Alumno | |
| Ministerio de Educación, Cultura y Deporte. Año 2001 | |
| Alumno |